qta4722のブログ一覧

なーんか、まだ数字の事を考えていました。

なんか、、こう、、１０÷３　の答えを、　ばーんと、　スパッと表す、
ミラクルな数値表現はないものかと、、、。
(このブログは先日の どうして10は3で割り切れないの？ の続きです。)

ぼーーーーっと考えてまして、
ふと思い出したのが、『尺貫法』　です。


尺貫法で行くと
１００ｃｍ　＝　３．３尺　　　なんですよね。


ということは、
１０ｃｍ　＝　０．３３尺　（←３寸３分のこと）


ということは、、、両辺を　３分の１　にすると、、、、

３．３３３３３３３、、、、＝　０．１１尺　（←１寸１分のこと）




おお。。。
１０ｃｍ　の　３分の１が、１寸１分　になってますよ。。。



同じことですが、
尺から１寸１分の長さを計算してみますと、、、

３．３尺　＝　１００ｃｍ　なので　１００ｃｍ÷３．３をすると、

１尺　＝　３０．３０３０３０３０．．．．．．ｃｍ

１寸　＝　３．０３０３０３０３０３０．．．．ｃｍ

１分　＝　０．３０３０３０３０３０３．．．．ｃｍ

なので、『１寸１分』　を普通のｃｍで表わすと、
１寸　＋　１分　＝　３．３３３３３３３３３．．．ｃｍ


だって、
１０　÷　３　＝　３．３３３３３３３３３．．．　ですもんね。。。


なので、
１０　÷　３　の答えは、　『１寸１分』　　ですね！！！




数字って、、歴史って、、、奥が深い。。。。
考え方、計算方法、おかしな点あれば、どんどんご指摘ください。。。

※　尺のＷｉｋipedeia

これが、昔、ずーーーーーーーーーーーーーーと疑問に思っていました。


小学校の頃からです。

１００ｇのチョコレートを、3等分すれば、ちゃんと3等分できているんじゃないの？
じゃあ、なんで３で割り切れないの？

というのが、疑問の発端です。


兄に質問すると、図面のようなことを教えてくれました。

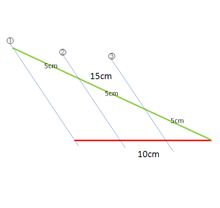
赤い線で１０ｃｍの線があります。
緑の線で１５ｃｍの線があります。

１５ｃｍの線は、５ｃｍずつで、きれいに3等分できますよね。
（適当に作った図なので計らないでください。。）

１０ｃｍと１５ｃｍの先端をつなぐ線①（水色）をひきまして、

それと平行線になる線を、
５ｃｍごとにびよーっと引けば、②、③の水色の線、

１０ｃｍが綺麗に3等分できるよ。


なるほどー。
と思ったのですが、
ますます、
じゃあ、なんで１０は３で割り切れないの？

と気になって仕方がなく、

小学校の頃の担任の先生に聞きました。

先生の答えは、
『１０は３で割り切れないんだから、本当に３等分できているように見えても、本当はできていないんだ。どこまでもどこまでも小数点で近付くように見えても、本当は3等分できてないんだ。』
でした。


。。。
どうも納得が行かなかった小学校の頃のｑは、
中学校になっても、担任の先生に同じ質問をしました。

中学校の先生は、
『だから　”3分の1”　という表現があるんだよ。』
と教えてくれました。

それでも、
そうなのか！とまで、納得できず。。。

のちのちもずーーーーーっと気になっていたのですが、

大学になってから、情報処理の勉強をしていた頃にですね、
２進法だの、なんとか進法だの出てきたんですね。

その時に思ったのです。

そうか。


１０ｃｍの物を３等分、できるし、１０を３で割った結果は、間違いなくあるのに、存在するのに、

１０進法では、１０を３で割った結果は、
線でいうなら、１０ｃｍを３等分しているポイントが、

１０進法では表現できない場所なんだ。

でも、１０を３で割った場所は確かにあって、存在してて、

中学校の頃の先生が言った、
『だから　”3分の1”　という表現があるんだよ。』
という言葉を、

そこで初めて理解した、
気分がしました。


なんで１０は３で割り切れないの？の
納得のいく答えは、
自分の中では、

『１０は３で割り切れるけど、１０進法では、その結果を表現できる数値がない。』

です。










こんなことを悩んでたなんて。。。



でも、そう思った後は、

１０を３で割った答えは、確かに存在しているけど、
小数点でどれだけ近付いても表現できない、という、

その存在というか、ポイントというか、

そこが、妙に大好きになりました。