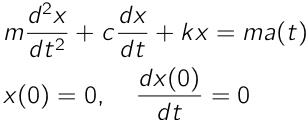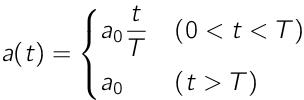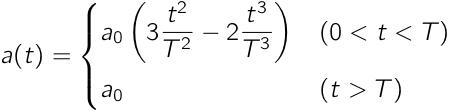theory_and_practiceのブログ一覧

諸々の背景の説明は省略させて頂くことをご了承下さい．
また，トラックバック先の記事は大いに参考にさせて頂きましたので，ご参照頂ければと思います．

この記事は，マツダのi-DMが用いているバネマスモデルを，2種類の入力（f = 質量m × 車の加速度a）を仮定して解いてみたというものです．

今回は，停車状態からの発進を想定して，質点（乗員）の変位xと速度dx/dtの初期条件として，ともにゼロを仮定しています．

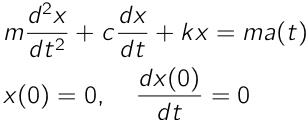
また，質量は人間の頭を想定してm = 5kg，減衰係数はc = 10N·s/m，ばね定数はk = 500N/mを仮定します（cとkは適当に決めましたw）．

1つ目に仮定する車の加速度は，1次関数で立ち上がるものとします．

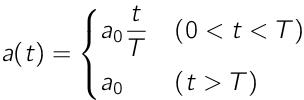
これは，たぶんi-DMが緑に点灯するんじゃないかな〜ということで，Greenと呼びます．

2つ目に仮定する車の加速度は，3次関数で立ち上がるものとします．

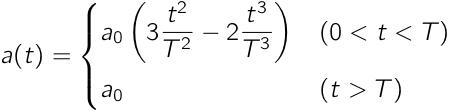
これは，たぶんi-DMが青に点灯するんじゃないかな〜ということで，Blueと呼びます．

これらは，時刻t = T = 2[s]で加速度a0 = 3[m/s^2]（約0.3G）まで立ち上げることを仮定してプロットすると，以下のようになります．

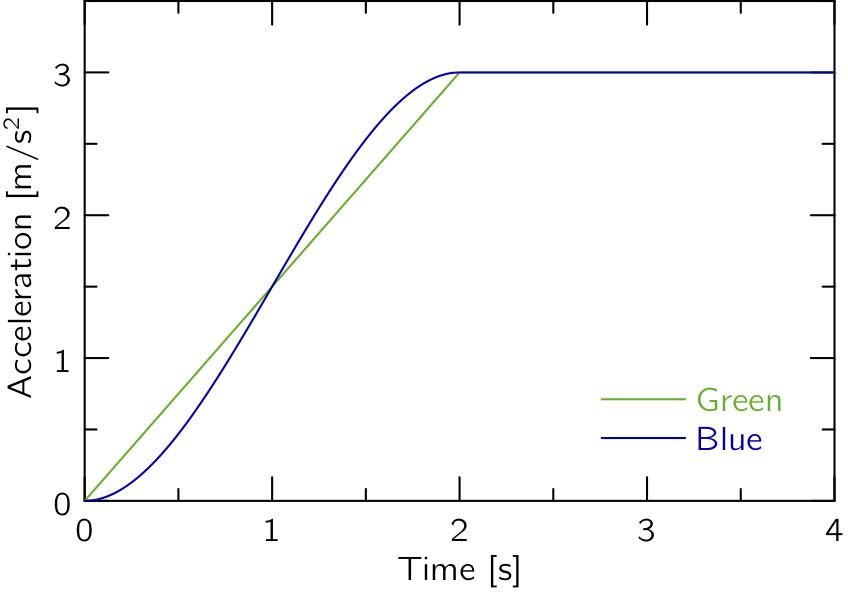
Blueは加速度の変化が滑らかになっているのが分かります．

対応する車速をプロットすると，以下のようになります．

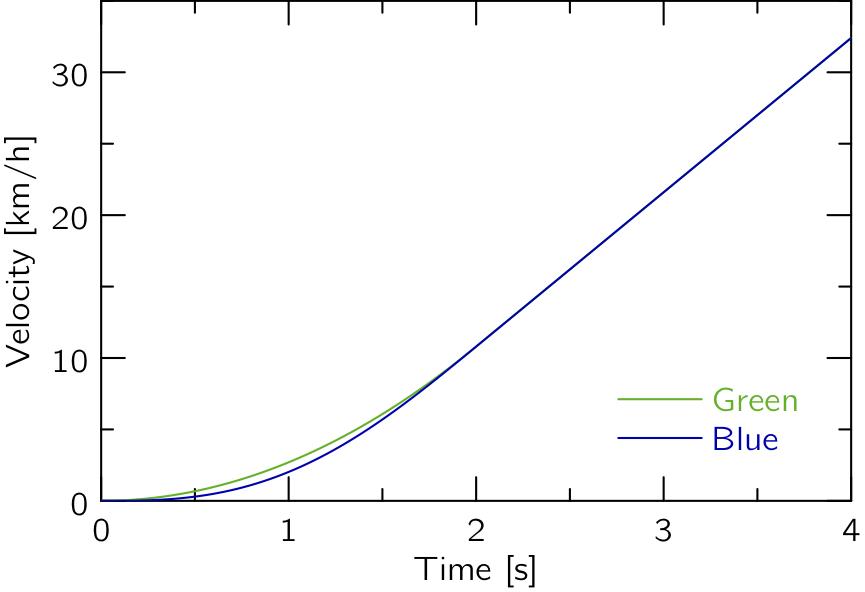
Green，Blueともに，t > 2[s]における車速は同一となります．

また，誤解の多い（笑）躍度（加加速度）をプロットすると，以下のようになります．

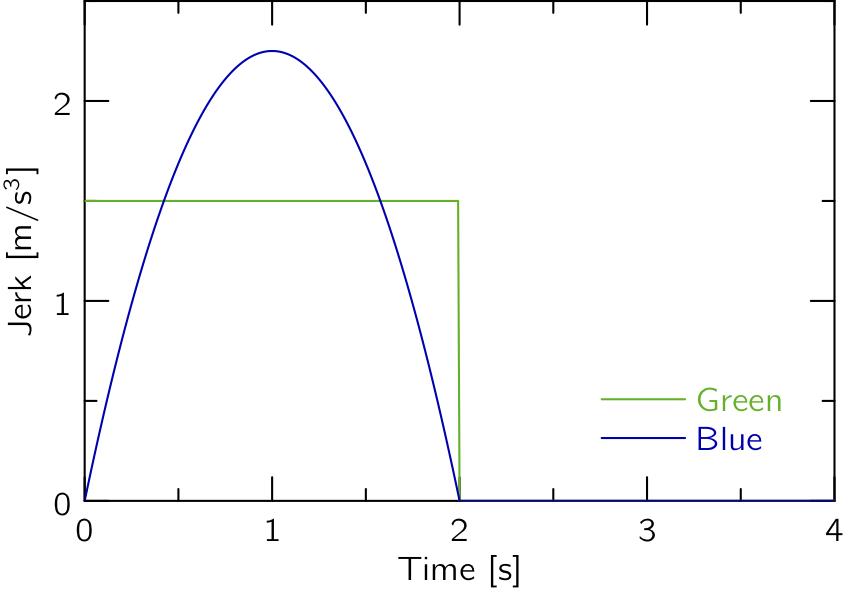
Blueのほうが，躍度のピークが大きくなっています．
あれ，躍度が大きいと荒い運転じゃないの？という疑問が湧いてきます．

しかし，はじめに示したバネマスモデルの運動方程式を解いて，質点（乗員）の変位xをプロットすると，以下のようになります．

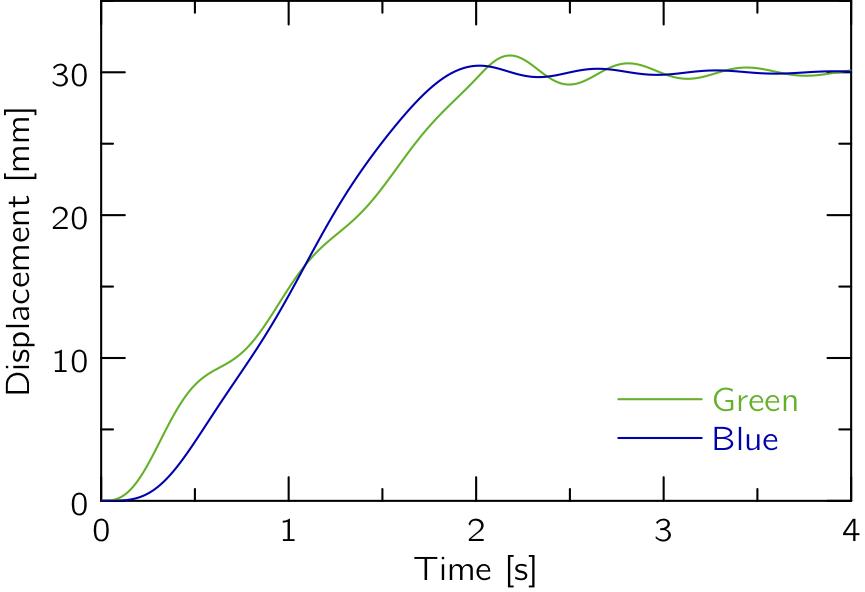
Greenでは若干の振動が発生しているのに対して，Blueでは振動が抑えられているのが分かります．

ということで，躍度が大きくても，加速度が滑らかに変化していれば，同乗者が快適に過ごせるのが分かりますね．