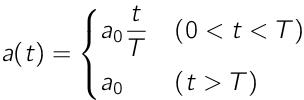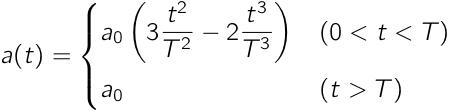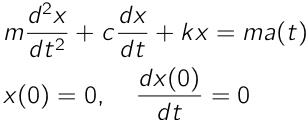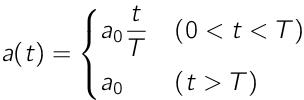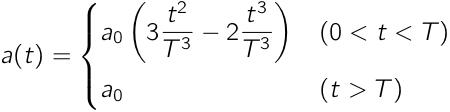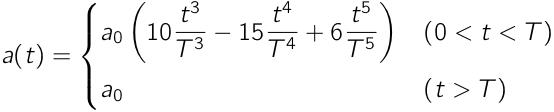theory_and_practiceのブログ一覧

MX-30 EV MODELのドライバビリティが良いとの評判なので、試乗してきました。
いつもお世話になっている販売店さんでは試乗車を置いていなかったので、少々申し訳ない気持ちを感じつつ、隣町のオートザムで試乗させて頂きました。

走る
第一印象は、めっちゃ普通😅（良い意味で）
私は普段SKY-Xを積んだMAZDA3に乗っているのですが、EV MODELの運転感覚はその延長線上にあると感じました。
普段SKY-Xに乗っている人が同排気量のSKY-Gに乗り換えると感じると思うのですが、Xの美点は、低回転域からトルクが出ていてリニアリティも高いところだと思うのです。
EV MODELの場合、それより一層、力強くて滑らかになるのですが、味付けとしては延長線上なので、違和感が無い。
例えば、減速後の再加速の操作も、SKY-Xと同様の感覚で青1ランプを楽に付けられました。

曲がる
EV MODELはSKY-Xよりも断然フロントが軽いためなのでしょうが、曲がるのが楽でとても楽しい。
当然、青1ランプも楽勝です。
この良さが、ロータリーを積んだシリーズハイブリッドにも受け継がれると良いんだけどなあ。。
ただ、街中での試乗のみだったので、パーシャルスロットルでの旋回性能は試せませんでした。
普段乗っているMAZDA3がAWDで、MX-30 EV MODELはFFのみ。
このようなシーンでは、後輪にトルクを配分できるAWDの方が有利なはずですが、比べてみたかった。

止まる
ブレーキは当然バイワイヤですが、協調回生ブレーキはSKY-Xのそれと同様、違和感が無い。
SKY-Xの場合、減速中にエンジンが停止する前後でのG変化をなるべく滑らかにするために、ブレーキングには多少気を遣う必要があるのですが、EV MODELの場合は、そのような気遣いは不要。
短い試乗の間でも、「楽だなあ」と感じてしまいました😅

聴こえる
SKY-Xのもう一つの美点として、低回転では静かながら、回せば勇ましいエンジン音だと感じています。
SKY-G 2.0のエンジン音は、ちょっと無味乾燥のきらいがあるので😅
で、EV MODELの疑似エンジン音は、直接聴いても中々に味わい深いものがあり、好印象でした。
あとは、毎日聴いても飽きないかどうか、車内で聴く音楽（私は大抵、車内ではクラシックの室内楽を聴いている）の邪魔にならないかがポイントかなあ。

納車されてから約4700km、ハイオクだけで走ってきましたが、唐突にレギュラーで走ってみたくなったので、今日初めてレギュラーを給油しました。
燃料を切り替えた直後の新鮮な感想を残しておきます。
（後で、ディーラーの担当者さんに教えてあげようw）

まず、2000回転以下のトルクは、レギュラーを入れたときの方が明らかに大きいです。
これは、ガソリンスタンドから走り出す段階で分かりました。
また、走り慣れた登り坂でも、グイグイ登ってくれるのを感じました。
給油直後で車重が重くなっていることを加味すると、低速トルクの差は体感以上かもしれません。

一方、トルクのピーク値に関しては、ハイオクとの違いがよく分かりません。
ハイオクの場合、2000回転以下と3000回転辺りのトルクの差が大きいので、スポーツモードにすると「トルクもレスポンスも良くなる」のが感じられるのですが、レギュラーの場合、ハイオクのとき程の差は無いので、スポーツモードの楽しさがあまりありません。
もしかしたら、トルクのピーク値は、ハイオクよりレギュラーの方が低いかもしれません。

細かなアクセルワークに対するレスポンス、リニアリティ、回転の滑らかさは、レギュラーにすると少し落ちる感じがします。
スポーツモードが楽しくないのは、そのせいもあるかもしれません。
ただ、トルク程の明らかな違いではないので、もっと乗り続けないと分からないかもしれません。

エンジン音に関しては、レギュラーの方が少し大きい気がしますが、これも僅かな違いなので、本当に大きくなっているのかは、ちゃんと計測しないと分かりません。

燃費に関しては、いつもハイオクで18.5km/Lぐらい出る道が、レギュラーだと17.5km/Lぐらいだったので、燃料代で言ったら同程度です。

今まで，2回ほどi-DMのバネマスモデルに関して考察を行ってきました．
第1回：i-DMのバネマスモデルを解いてみた
第2回：i-DMのバネマスモデルを解いてみた2：滑らかな躍度変化，立ち上げ時間
以来，仕事が忙しくて後回しになっていたのですが，最後にもう一つだけ，やりたいことがあったので，今回はそれについて書きます．

i-DMに関しては，普通に時間領域で議論されることが多いようですが，工学部（特に機械科，電気科）を出た人にとっては，周波数領域の方が馴染みやすいものと思います．
ですが，文系の人には分かりにくいだろうなーと思い，躊躇していましたが，まあ分かる人にだけ分かって頂ければいいやと思い，今回の投稿に至りますw

基本的には，第1回の内容を周波数領域で焼き直すものなので，ご参照下さい．

バネマスモデルの運動方程式は，周波数領域では以下のように表されます．

前回，前々回と同様，質量は人間の頭を想定してm = 5kg，減衰係数はc = 10N·s/m，ばね定数はk = 500N/mを仮定します．
また，ω = 2πfは角周波数（fは周波数），iは虚数単位（i^2 = -1）です．

上記の運動方程式は，時間領域と違って単なる代数方程式なので，以下のように簡単に解けます．

この解の意味するところは，変位xを周波数領域で表すと，伝達関数Hと車両加速度aの積で表されるということです．
時間領域だと，こんなに簡単には表せませんので，周波数領域での議論は分かりやすいのです．

伝達関数は複素数となりますが，その絶対値をプロットすると，以下のようになります．

角周波数ω = sqrt(k / m) = 10 rad/s，周波数にして約1.59 Hzで共振する特性であることが見て取れます．
したがって，振動を抑えるには，この周波数成分の車両加速度を抑えることが有効です．

続いて，時間領域で以下のように表される車両加速度をGreenとします．

また，時間領域で以下のように表される車両加速度をBlueとします．

これらを，時刻t = T = 2[s]で加速度a0 = 3[m/s^2]（約0.3G）まで立ち上げることを仮定してプロットすると，以下のようになります．


Greenの車両加速度を周波数領域で表すと，以下のようになります．

一方，Blueの車両加速度を周波数領域で表すと，以下のようになります．

なお，これらの第1項は，周波数ゼロで無限大となるデルタ関数ですので，これを除いてプロットすると，以下のようになります．

Greenは角周波数の2乗に反比例して減衰するのに対して，Blueは各周波数の3乗に反比例して急峻に減衰することが分かります．
厳密に言うと，これらは振動しながら減衰していく特性ですが，伝達関数の共振周波数である1.59 Hzで比較すると，やはりBlueの方が小さくなっています．

以上に示した伝達関数と車両加速度の積を取ることで，周波数領域の変位を求めると，以下のようになります．

やはり，GreenよりもBlueの方が全体的に変位が小さくなっていることが分かります．

なお，周波数領域で見たとき，車両加速度には周期的にゼロ点が存在するので，上手いことこのゼロ点と伝達関数の共振周波数を合わせるように立ち上げ時間を調節することで，変位を小さくすることも可能と考えられます．
本当に上手い人は，この辺も考えて運転操作できるのかもしれませんが，繊細なアクセルコントロールが必要なので，難しいものと予想します．

この，些か机上の空論的なシリーズは，一応これで最後のつもりです．
読んで下さった方々，どうもありがとうございました．

誰が読んで下さるのか分かりませんが，備忘録として書こうかと思います．
（Facebookとかに書かずにこちらに書くのは，少しは読んで下さる方がいらっしゃるかなという期待があるからのですが^_^;）

初めてにして今のところ唯一のマイカーであるデミオの1.5Dが3年目の車検だったので，ついでに商品改良したばかりのCX-3の2.0Gと1.8Dに試乗しました．
また，代車はアクセラの1.5Dでした．
単純に，乗った順に書きます．

CX-3 2.0Gの感想

とりあえず，エンジン音がディーゼルと大分違って甲高いので，ディーゼルにしか乗ったことない私としては，ちょっと違和感ありましたw
それはさておき，さすがNAガソリンエンジンは，ゼロ発進からのレスポンスが素直で楽ですね．
i-DMの5thステージで白を出さない運転に固執する癖がついてしまったので，すっかり青1発進が苦手になってしまいましたが，ガソリンならそれほど苦なく青1発進できました．
しかも，前が軽い分，ハンドリングも軽やか．
GVCも初体験でしたが，かなりイージーモードになっているのはハッキリわかりました．
普通ならアクセルを軽く抜かないと綺麗に曲がれないところを，オートマチックにやってくれるのは楽です．
カックンブレーキが起こりにくいのは，後輪がディスクブレーキだからかな？
サスとタイヤが次世代技術の要素が取り入れられて，操安性と乗り心地を両立できるようになったとのことですが，普段走っている道とは違うので，単純比較はできませんでした^_^;

CX-3 1.8Dの感想

基本的には1.5Dを踏襲しているだけあって，エンジン音からして，圧倒的な安心感w
短い試乗では，青1発進は出せませんでしたが，扱いやすさは大分向上していると感じました．
ハンドリングは，やはりデミオの1.5Dと同系統と感じましたので，GVCによる挙動は，「自分が物凄く丁寧にデミオを運転したらこうなるだろうな」という感じのものでした．

アクセラ 1.5Dの感想

さすが，デミオより1クラス上だけあって，同じ1.5Dでも静粛性が上ですね．
でも，車重が重い分，エンジンが苦しそうw
ゼロ発進時は，じゃじゃ馬そのものですが，何せ3年乗った1.5Dですから，その手懐け方も慣れたものですww
右足に神経を集中させて，狙い通りに発進できたと感じた時は，自ずと青1が点きます．
別に，条件によってレスポンスが変わる1.5Dで青1発進させることに，何も意味が無いと思っていますけどね．
例え青が点いても，ドッカンターボが出たんじゃ，本末転倒ですから．
職場に向かう道でS字カーブっぽくなっている交差点があり，ここが腕の見せ所だと勝手に思っているのですが，GVC搭載車だと，悲しいくらい上手に曲がれて，何とも言えない気分になりましたwww

というか，私のドラテクの程

3年前にペーパードライバーを引退してから，i-DMだけを頼りに特訓してきました．
まあ，仕事で数学をバリバリ使うので，理屈は分かっているつもりです．
（専門は機械ではなく，電気ですが）
ただまあ，些か自己流なのだと思っています．
i-DMの指標でいうと，一応，アクセル，ブレーキ，ハンドルともに，青2は無問題ですw
青1アクセルは，コンディション次第ですかね．意のままに1.5Dを操るのは，やはり難しい^_^;
青1ハンドルは，走り慣れた道なら大丈夫ですが，アクセルとブレーキとの協調がまだ甘いためか，ちょっとした交差点でも，まだまだ出せません．
青1ブレーキは，理屈は分かっていますが，安全運転の範疇では出せたことないです．
安全上のやむを得ぬ理由で，丁寧に急ブレーキ（苦笑）を踏むと，青1になります（苦笑2回目）
多分，それなりの加速度変化があると，滑らかさの判定が甘くなるからなのでしょうが，もっと上手になれば，普通に青1ブレーキが出せるようになるのかな？

前回の記事「i-DMのバネマスモデルを解いてみた」では，加速度を滑らかに立ち上げることで，発進時の振動が抑えられることを示したました．
ここでいう「滑らか」の数学的な定義は，「1階微分が連続」ということなのですが，つまりは「グラフに折れ曲がった部分が無い」ということです．

今回は，加速度が「2階微分まで連続」となる場合を取り上げます．
これは，タイトルの通り，「躍度変化が滑らか」となることを意味しています．
また，立ち上げ時間と振動の関係についても述べます．

前回と同様，停車状態からの発進を想定して，質点（乗員）の変位xと速度dx/dtの初期条件として，ともにゼロを仮定します．

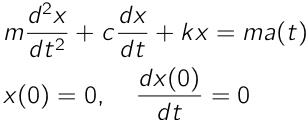
前回と同様，質量は人間の頭を想定してm = 5kg，減衰係数はc = 10N·s/m，ばね定数はk = 500N/mを仮定します．

車両加速度a(t)の例として，1つ目は1次関数で立ち上がるものとします（前回と同様）．

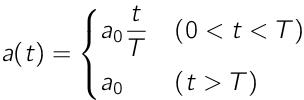
前回は「Green」と読んでいましたが，今回は「Linear（1次）」と呼ぶことにします．

2つ目に仮定する車両加速度は，3次関数で立ち上がるものとします（これも前回と同様）．

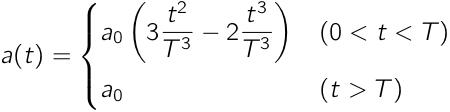
前回は「Blue」と読んでいましたが，今回は「Cubic（3次）」と呼ぶことにします．
なお，これはt = 0, Tにおいて，1階微分が連続となります．

今回新たに導入する，3つ目の車両加速度は，5次関数で立ち上がるものとします．

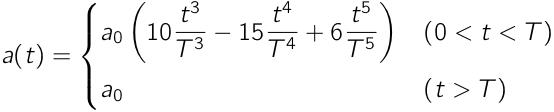
これを「Quintic（5次）」と呼ぶことにします．
なお，これはt = 0, Tにおいて，1階微分と2階微分が連続となります．

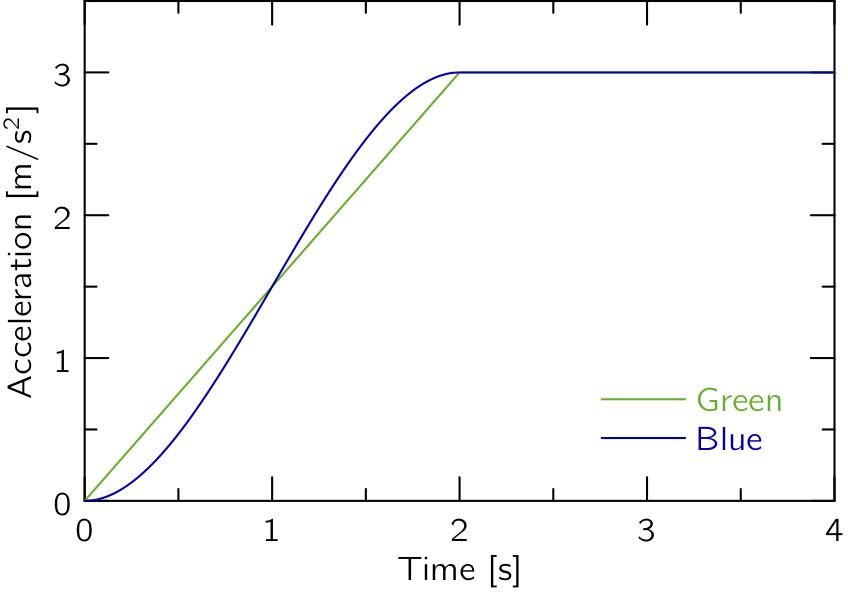
これらは，時刻t = T = 2[s]で加速度a0 = 3[m/s^2]（約0.3G）まで立ち上げることを仮定してプロットすると，以下のようになります．

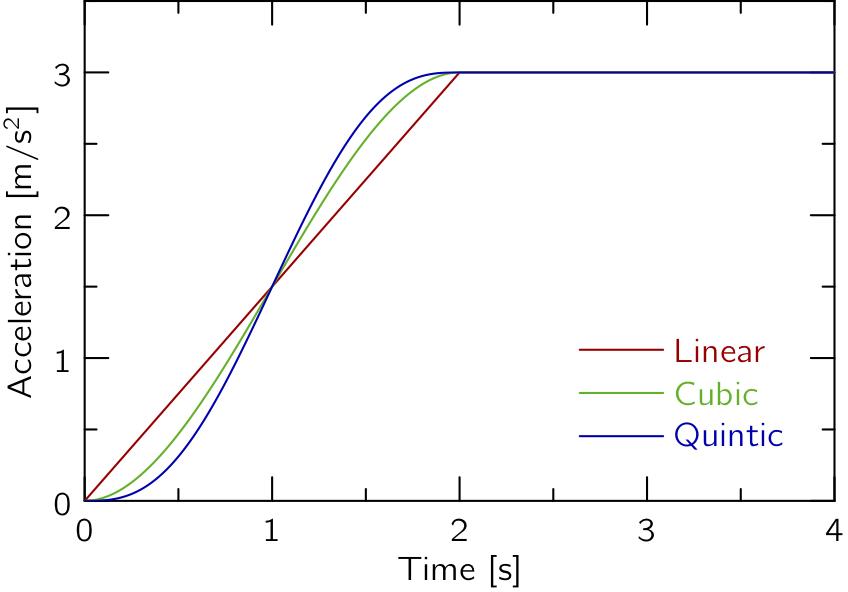
Linearはt = 0, 2[s]で折れ曲がっているのに対して，CubicとQuinticは滑らかとなっています．

対応する車速をプロットすると，以下のようになります．

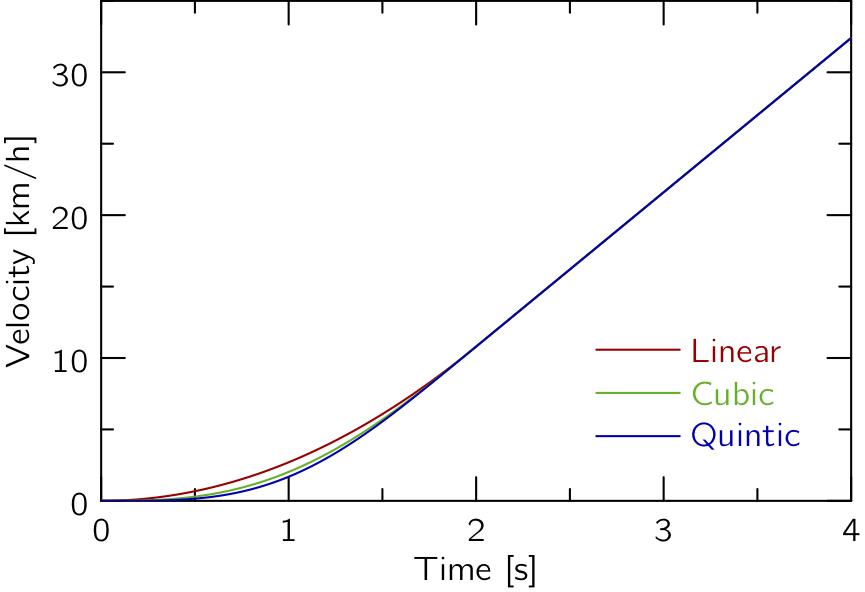
Linear，Cubic，Quinticともに，t > 2[s]における車速は同一となります．

対応する躍度（加加速度）をプロットすると，以下のようになります．

Linearではt = 2[s]で不連続となっているのに対し，Cubicは連続になっています．
さらに，Quinticでは単に連続なだけではなく，至る所で滑らかな曲線になっているのが分かります．
また，躍度のピークはLinear→Cubic→Quinticの順に大きくなります．

これらの加速度を入力としてバネマスモデルの運動方程式を解いて，質点（乗員）の変位xをプロットすると，以下のようになります．

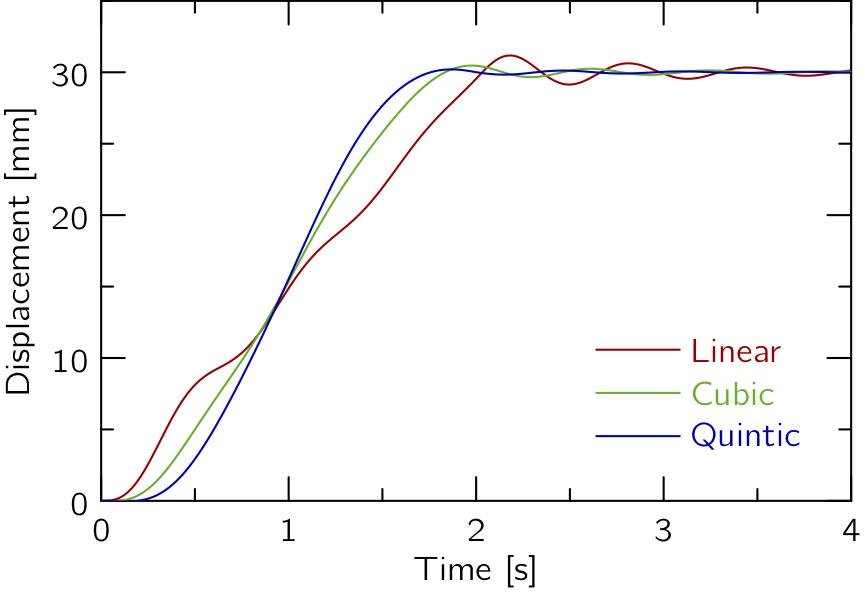
Linear→Cubic→Quinticの順に振動が小さくなっているのがお分かり頂けるでしょうか？
CubicとQuinticの違いが分かりづらいですねw

ということで，変位の振動成分（実際の変位から，入力とバネの反力が静的に釣り合う位置x = m a(t) / kを差し引いたもの）をプロットすると，以下のようになります．

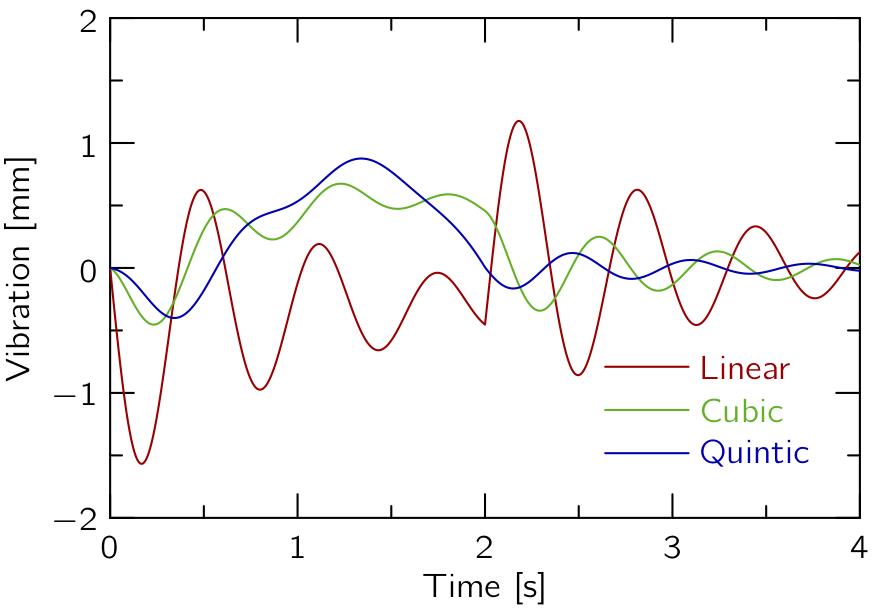
CubicとQuinticを比べると，ピーク値ではQuinticが大きいものの，細かい振動はQuinticの方が抑えられているのが分かります．

さらに，立ち上げ時間Tと，t = Tにおける振動の振幅の関係をプロットすると，以下のようになります．

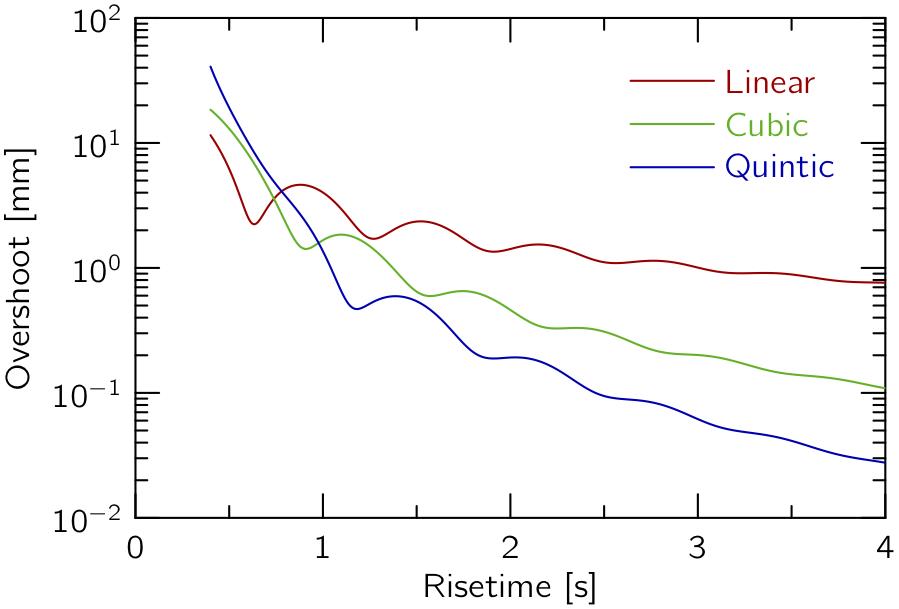
立ち上げ時間Tを長くすると振動が小さくなるのは全てのパターンで共通していますが，Quinticは立ち上げ時間の増加に伴って，最も早く振幅が小さくなっていくのが分かります．

ということで，「躍度の時間変化は滑らかな方が望ましい」という結論が得られます．
言い換えれば，「加躍度もしくは加加加速度wは連続である必要がある！」ということになります．

はい，結局，今回は「加加加速度」というフレーズを使いたかっただけですwww