 covid-19 / 🌰バイバイン🌰🌰
covid-19 / 🌰バイバイン🌰🌰 
この米粒が30日後には、ものすごい数になるんです。
計算してみましょう。
約60,000粒=1升
として、
40升=1俵(60kg)
とすると、
nーー2の29乗(初日が2粒でなく1粒なので2の0乗。だから30日目は29乗)
=536,870,912粒
=約8,192升
=約256俵
当時、1人が一年間で食べるお米は約1俵だったので、256年分のお米に匹敵します。
この256俵は30日目にもらうお米で、1日目〜29日目までも加えた30日間にもらう米の合計は448俵くらいになります。
5人家族としても、約80年分ですね。
指数関数恐るべし
秀吉は、途中でこれが天文学的な数で、とうてい与えつづけることはできないことが分かり、褒美を他のものに替えてもらったそうです。
あなたは新聞紙を100回折り畳むことができますか?
100回折ったら厚さはどれくらいになるでしょうか?
また、月までの距離である38万kmにするには何回折ればいいと思いますか?
(まぁ、物理的には10回でさえ折れないとされていますがね)
1回折ると、重なる枚数が2倍になるので、例えば3回折ったときの重なる枚数は
2×2×2(=2の3乗)=8と計算できます。
さて10回折ったらどうでしょう。
2の10乗(=1024)をおよそ10の3乗(=1000)とします。
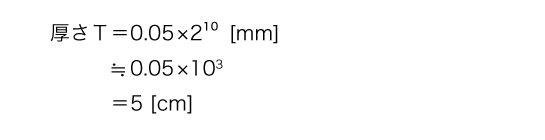
では100回折ると?

では38万kmにするには? 答えは高々43回です。

初期値がいくら小さくても、倍々にしていくと、あっという間にものすごい数になります。
こういう性質を持った、

という関数を指数関数といいます。
 円の3等分 🍰
円の3等分 🍰 |
Re: 👦👧 車の周りの子供たち 🧒👶 カテゴリ:その他(カテゴリ未設定) 2023/05/03 20:32:33 |
 |
|
『取替 と 取換 と 交換』🐸 カテゴリ:その他(カテゴリ未設定) 2023/05/03 20:32:10 |
 |
|
車庫証明、貼ってますか? 🅿️ カテゴリ:その他(カテゴリ未設定) 2023/05/03 20:31:53 |
 |
 |
ランドローバー フリーランダー2 FINAL EDITION , 2000cc DOHC TURBO 4WD |
 |
その他 ルイガノ LGS-VES D 【2007年5月購入】 変速、サスペンション、ライトを電子制御するフルオートマチック ... |
 |
ランドローバー ディスカバリー3 【軽量・軽装備のグレード”S”を敢えて選択】 V8への憧れはありましたが... ・HS ... |
| 2023年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2022年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2021年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2020年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2019年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2018年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2015年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2014年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2008年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2007年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2006年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2005年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2000年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |