aki@rsのブログ一覧

少し前ですが結構足回りの話を書いてたので、記事を集めると基礎的な部分をそこそこ網羅してるんじゃないか？と思えてきました（笑）
ここで言う「基礎的な部分」というのは、例えば自動車操縦安定性講座入門とかサスチューニングの理論と実際とか車両運動性能とシャシーメカニズムとかそういうので基本として扱われてるような部分のことです。

そんなわけで「足回りの基礎」ってカテゴリ作って、もろもろブチ込んでみました（笑）
「これから足回り勉強したいけど、とっつきにくい本は嫌だなぁ～」って人などに、足回りの知識に関心を持ってもらう上で少しでも役に立てばと思います。
あくまで「関心を持ってもらう上で」というレベルなので、真剣に勉強したくなった方は上記参考文献などをご覧下さい。
あと、いくつか足りてない項目があるので、少しずつ追加していきますね^^

さてみなさん「コンプライアンス」というと何を思い浮かべますか？
「法令遵守」って耳が痛いんじゃないでしょうかね（笑）
今日はサスペンションのゴムのお話のほうです。
この場合のコンプライアンスとは「物体に力が加わって変形すること」というような意味です。







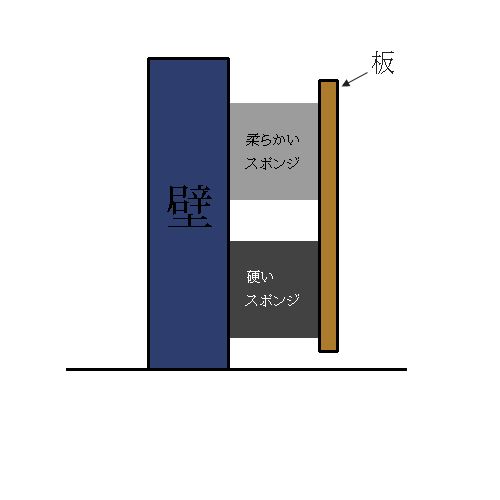
ところで上の図を見てください。
壁と板の間にスポンジが挟まっています。
薄いグレーのスポンジは「柔らかいスポンジ」です。
もう、ふにゃふにゃです！
それに対して、濃いグレーのスポンジは「硬いスポンジ」です。
ぐぐーっ、って大きな力をかけないと潰れません。

さて、ここで板の真ん中を押してみると、どうなるでしょうか？







柔らかいスポンジは潰れやすいので、板が斜めになりました。
いいですよね。
板はさっきまで壁と水平だったのに、横から力を加えたら、斜めになりました。
これが大事です^^

で、今度は、こういう形のアームがありまして、







この空洞のところにゴム製のブッシュを入れて、






これを２本、サスペンションメンバに取り付けます。











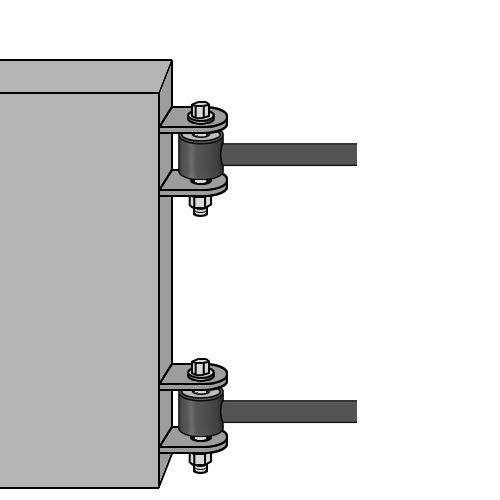
アームの反対側には（ハブを介して）タイヤが取り付けられます。
とりあえず、これをクルマのサスペンションに見立ててください。







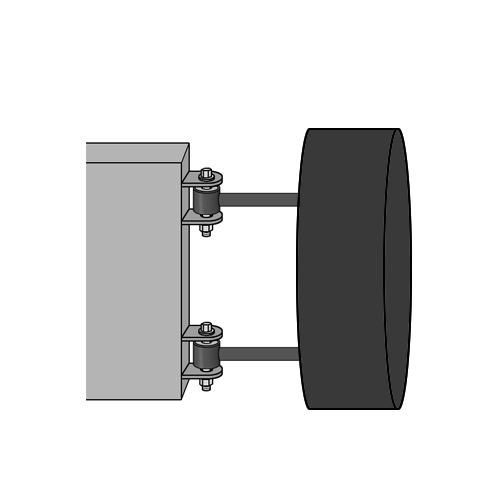
ところでクルマが左カーブを曲がるとき、左にハンドルを切ると、右側に横Ｇがかかりますね。
クルマ自体は遠心力によって右側（コーナー外側）へ向かおうとするのに、タイヤはグリップ力によってその場に留まろうとしますから、タイヤには「車体側へ押される力」がかかっています。
分かりますかね、例えば氷の上を走るときのようにタイヤが「つるーっ」と滑ってしまったときは、この力はかかりません。
タイヤがグリップすることにより、タイヤが車体側へ押される力が生まれます。
自動車工学の世界ではこの力を「横力」と言い、また「車体に対して内側方向にかかる力」のことを「内引き方向の横力」と言います。

勘のいい方はすでにお分かりかもしれませんが、内引き方向の横力がかかった状態と、一番最初のところで出てきた壁＆スポンジ＆板の例は、同じようなことを表しています。
サスペンションのゴムブッシュはスポンジほどは柔らかくないので、まったく同じでもありませんが、金属と比べれば柔らかいという意味では似ています。
つまり、ゴムが柔らかいほうが変形してたくさん潰れるし、ゴムが硬いほうがあまり変形せず潰れない、ふたつの硬さに差があれば、板が傾くのと同じでタイヤが傾きます。










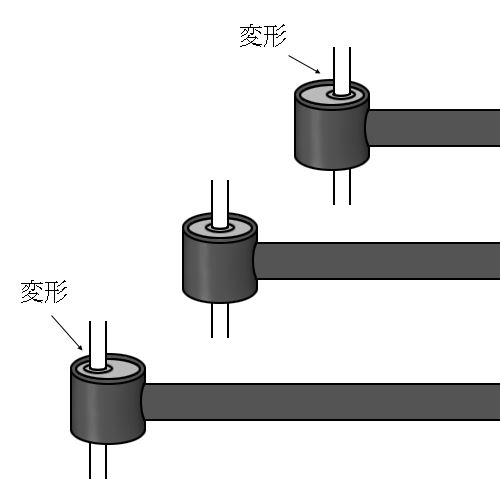
タイヤは、内側を向けば「トーイン」、外側を向けば「トーアウト」ですね。
どのくらいの硬さのブッシュを使うかによって、横力によるトーイン/トーアウトを制御しようというのがコンプライアンスステアです。

ロードスターのリヤサスペンションに関しては「トーコントロールサスペンション」と呼ばれているので、そういう呼び方で知っている方も多いかもしれませんね。
実際は上のような２点支持のモデルとは違い、アッパーアームを含めた３点支持になっています。
またNA/NBロードスターの場合、ロアアームは２本ではなく一体もののＨ型アームが採用されています。

このリヤサスペンションについては、内引き方向の横力でトーイン、外引き方向の横力でトーアウトです。
したがってアンダーステア方向になるようにセッティングされていると言えます。
これを例えば前後のブッシュの硬さを揃えたりすれば、横力トーインをなくすことが出来ます。
金属製のブッシュ（ピロボールブッシュ）を使っても同じです。
ゴムによるアンダーステア方向のセッティングをキャンセルすることになるので、つまりオーバーステア傾向になります。

横力トーインの量はNA型ロードスターのほうがNB型ロードスターより多く、NB型へのモデルチェンジの際に変化量を小さくしたそうです。
理由は「あんまり大きく動くと、なんか変な感触だから」だそうです。

ところで「トーコンキャンセラー」という商品があって、NA/NBロードスターのリヤアッパーアームのハブ側ブッシュを硬質ウレタンなどに交換しますが、この部分を交換しても横力トーインの量は少ししか変わらないと思います。
本来の意味合いでトーコンをキャンセルしたいなら、ロアアーム車体側ブッシュの「前後の硬さを揃える」のが効果が高そうですね。
ただ、トーコンキャンセラーでも、キャンバ変化は結構減ると思います。
「トーコンキャンセラー」という呼び方が正しいかどうかは分かりませんが、何かしらの効果はありそうです。
具体的にどの部分がどう変化するのか、そのあたりをじっくり考えてみると、ブッシュ変形によるアライメント変化…つまりコンプライアンス系のセッティングが身近に感じられるかもしれませんね^^

「コーナーの一番Ｇがかかるところでスピンしにくくしたい」
「曲がり始めから立ち上がりまで、ずっと同じように曲がりやすくしたい」
「とにかく少しでもアンダーステアにしたい」

初期値としてのアライメントと、横力がかかったときのアライメント変化、そのふたつを考えながら、いろんな目的に応じたセッティングが出来るとよいですね。
ブッシュを硬くしてけば、アライメント変化は減る方向です。
またタイヤのグリップ力が上がると、横力が増えるので、アライメント変化は増える方向です。
さぁ、あなたの希望する組み合わせは…どんなでしょう？^^

ちなみにですけど、今回のコンプライアンスステアのお話とロールステアのところで出てきたジオメトリのお話を組み合わせると、タイヤ前引きや後ろ引き時のアライメント変化も読み解けます。
つまり、加速時や減速時のトー変化です。
想像してみてね^^
（↑理屈が同じなので書くの面倒くさいだけとも言う。笑）

昨日のあほみたいなブログ（笑）に、ゆういっつあんから質問を頂きました。
「地面を掘らずにロールセンターより重心が低くなる事はあるんですか？」
そうですね、実際に販売されているクルマでは、そういうクルマはないと思います。
ないものは作ればいいので、それでは作ってみましょうか！^^








とりあえず確認です、クルマがありまして、







ロールセンタがこのへん。






次に、ボディをなくしてサスペンションメンバのみ与えられたクルマを用意します。
ちなみにこのクルマのメンバはドライカーボン製です。
軽くて丈夫！カーボン偉い！
いいなぁ～。
僕の自転車もカーボンで作ってほしいものです（クルマはいいのか。笑）

え！ボディをなくすと人間が乗れないって？
人間が乗れなければハンドルを切れないから困る？
あぁ、そうですね、鋭いですね、じゃあパワステモータをリモコンで操作できるクルマということにしませんか（笑）
ていうかラジコンじゃん（笑）

バネもないから水平を保てない…前後のメンバをつなぐ手段もない…。
とりあえず無視しましょう！（笑）






で、このクルマのロールセンタはこのへんですね。






例のように重りをつけますと、






重心がロールセンタより下に来ましたので、これでミッションコンプリートです♪
このクルマもやはり、右にハンドルを切れば右に傾くクルマになりますね。
ロールの方向は重心がロールセンタより上にあるか下にあるかで決まります^^

























今回の例ではロールセンタを上げるためにアームをすごく急な角度にしてみました。
実際はこれだといろいろ不都合があって、バンプ/リバウンドでトレッド変化が大きくなるし、ストローク時の側圧も大きくなるし、あとあとアンチリフトジオメトリのところで書いたのと同じ理屈で、ジャッキアップが大きくなります。
だからこんなクルマは販売されてないと思うんですけど、でもこういうクルマだと具体的に何がどうなるのか、なんで都合が悪いのかというのを考えて理解しようとすることはすごく大切なことだと思います。
素晴らしいですね。面白いですねー^^
いやぁ映画って本当にいいもんですねー（映画じゃねぇよ！笑）

あと、ついでですけど…。
「ロール中のロールセンタ」についても、この際なので触れておきますね。

クルマは直進状態からハンドルを切るとロールセンタを中心にロールします。
ところがロールセンタは常に一定とかではなく、アームの動きに合わせて移動します。
以前バンプ/リバウンドでの移動について書きました。
ロールによっても移動します。








青い点がロールセンタです。

少しハンドルを切った状態でカーブを曲がっていき、そこからさらにハンドルを切り足す場合…を考えると分かりやすいかもです^^
ある程度ロールしている状態では、ロールセンタは静止状態から少し移動した位置にあります。
そこからハンドルを切り足すと、その「移動した位置」を中心にロールが追加されます。

これは実際に絵を書いてみればそうなるので「そういうもの」と思って頂いて構わないと思うのですが、どうしても言葉の説明が欲しい場合は

「リンクによって円軌道で動く物体に、ある一定方向の力が加わった場合、その物体が円軌道のどの位置にあるかで、力の伝達の向きが変化するため」

…という感じで僕は考えています。
やー、なんか、小難しい言葉で説明するのって分かりにくいし嫌ですね^^;
やっぱシンプルなイラストと平易な言葉で説明するのが一番です（苦笑）

イラスト作るのが一番難しいんですけどねぇ～（笑）（笑）（笑）

クルマの重心は低ければ低いほどいいそうです。
僕も自分のロードスターの重心はもうちょっと低く出来たら嬉しいな～と思います。
実際にそれをしようと思うと、いろんな要素と兼ね合いになるので難しいです。
でもでもスポーツカーは重心を低くするのが基本ですね。

さてこの「重心は低くするのが基本」「重心は低ければ低いほうがいい」っていうところに、お茶目なakiさんは噛み付いてみました！
何でもそうですが「○○ければ○○なほどいい」という考え方は危険です。
「行き過ぎたらデメリットが出てくるのではないか？」と常に疑って、いろんな角度から物事を考えることが重要です！

いやでも…まんが「頭文字Ｄ」にも「重心は低ければ低いほどいい」って書いてあったし…エライ人たちも口を揃えてそう言ってるし…ごにょごにょ。
みんなそう言ってるから、これは流石に正しいに決まってる…

…という考え方は危険だって言ってるでしょ！（笑）
よし分かった、分かりました、しょうがないですね～もうっ。
ここはひとつ、天邪鬼なakiさんが「それは違うよ」と証明してみせましょう！

世界初公開！！
「クルマの重心は低ければ低いほどいい…わけではない、という説明」です！
いや世界初ではないと思うけど（笑）






まずは基本的な構成図からいきましょう。
タイヤと、サスペンションアームと、ボディです。







ダブルウィッシュボーンの場合、ロールセンタがこんな感じで決まるので、









クルマに横Ｇが加わったとき、ロールセンタを中心にロールしますね。
これは荷重移動があるからです。
荷重移動があるとタイヤの４輪合計のグリップ力が減りますので、嬉しくありません。

重心が低ければ荷重移動を減らすことが出来る、だから重心は低いほうがいい。
…というのが一般に言われている理屈だと思うのですが、ははは、甘いですよ。
コーヒーにお砂糖を３杯入れるくらい甘いです。
甘い甘いひとときです（なんじゃい。笑）







ふつう重心を下げようとして車高を下げていくと、ボディが地面とディープキスしてしまい、それ以上重心を下げることが出来ませんね。
でもでも、やろうと思えばそれ以上重心を下げることは出来ます。
いいですか皆さん！
いろんな角度から物事を捉えて、自由な発想で考えることが重要ですよ！






ってなわけで、


































地面、掘っちゃった♪（笑）




「あほかー！（笑）」って言われそうですけど、でもでもこれ実際に実現可能な手段ですから、僕間違ったことはひとつも言ってなi……げふげふっ！
いや違うんですよごめんなさいこれには理由があるんですお願いですから石を投げないで～(^▽^;)

とりあえずこれ冷静に考えてみますと（笑）、ボディの下に重りをつけてますから重心が下がり、地面の高さ以下になっています。
重心を下げるために余計クルマを重くする馬鹿がどこにいるんじゃあ～～、と怒られそうですが、だってボク「重心を低くする」としか言ってないモン！
だってだって女の子だモン！（あ、おれ男だった。笑）

重心を地面の高さ以下にできると仮定した場合、限度を超えると、重心を下げれば下げるほど逆に荷重移動量が増えていくことになります。
そんなこんなで重心は下げすぎても荷重移動量が増えますよ！
だから「低ければ低いほうがいい」とは言えないですよ！
以上、Q.E.D.証明終了！
でもでも実際はこんなことは起きないのでこの証明に特に意味はないです（笑）

ところで、これって面白いんですけど「ロールの方向」が逆転します。
わかります？
右にハンドル切るとクルマが右に傾くんです。
普通は右にハンドル切ったら、左にクルマが傾きますよね。










まぁ理屈は単純で、重心がロールセンタより下にくるからです。
普通のクルマではあり得ませんが、おかしなクルマを作ろうと思えば、あり得ることはあり得ます^^;

だってほら、バイクとかって、右カーブを曲がるとき、右側に車体が傾いた状態で釣り合ってるじゃないですか。
ボートとかも、右に曲がるとき、右に傾いた状態で釣り合ってるでしょ？
飛行機もそうですよね。
でもクルマはふつう曲がる方向と逆に傾くじゃないですか～。
これ、重心をロールセンタより低くすると、バイクとかと同じに出来るので、ちょっと面白いなと思って（笑）

まったく…単にそんなことを言うためにわざわざこんな訳の分からんことを…。
ははは、僕はただ「くすっ」と笑って頂けたらそれで本望ですよ（笑）

ちなみによく「重心とロールセンタ間の距離がゼロになればクルマはロールしなくなる」と言いますが、重心と地面との距離がゼロでない限り、ロールはしなくても荷重移動は起こります。
「ロールしない＝サスペンションのないクルマと同じ」、というだけで、例えばすごく大きな横Ｇを与えると、ロールはしなくても横転とかはしますよね。








重心高さ＝ロールセンタ高さ＝地面高さ、となるように作れば、ハンドル切ってもまったく荷重移動の起きないクルマの出来上がりです^^
これなら横転もしませんね。荷重移動がまったくないわけですから。
こんなクルマはあり得ないですけど、もしも実際に運転できたとしらどんな感触になるのか、ちょっと気にはなります…。
ロードスターの車高下げて、地面掘って、ボディに重りをくっつければいいだけだから、誰か試してみて下さい（お前がやれよ。笑）

まったく、自由な発想にも程があるぞ！
フリーダムすぎて頭がイっちゃってるとしか思えない！
あまりに自由過ぎるのも考えものだ、というわけで「○○ければ○○なほどいい」とは言えませんよという話…

というかアホなこと考えてみました、という話でした（笑）

皆さん摩擦円ってよくご存知だと思いますが、以前…数年前ですけど…インターネットでこんな記事を読んだことがあります。
個人の方が書かれたものです。





☆☆☆☆☆





タイヤのグリップ力には限界があり、そのタイヤが持つグリップ力を縦に100％使ったとしたら、横には使うことができない。
だからフルブレーキの最中は、ハンドルを切っても曲がらない。
タイヤのグリップ力が縦に50％だけ使っている状態なら、そこでようやく残りの50％を横に使うことが出来る。
縦に70％なら横に使えるのは残りの30％、縦に20％なら横に80％…。

これを実際グラフにしてみると、ちょっと待てよ、円にはならない。



縦に100％のとき、横に0％。
縦に50％のとき、横に50％。

だから、よく言う「摩擦円」というのはおかしい。
本当はダイヤモンド型だ！





☆☆☆☆☆





…といった趣旨の記事でした。
これを読んで、「なるほど！」と思った方も、「それは違うよ」と思った方も、「あれ、なんかおかしいな？？？」と思った方もいるかと思います。
が、僕にとっては衝撃的な記事でした。
この記事を書いた方が今まで読んできた摩擦円に関する説明は、どの説明も決定的に欠けているところがあったんだなと思うと同時に、もしもそういう説明が前提にあるとすると、このように考えることってある意味で素晴らしいことだな、と思ったんです。

結論から先に書きますと、このダイヤモンド型の図というのはＺ＝Ｘ＋Ｙ（ただしＺ≧０、Ｘ≧０、Ｙ≧０）という数式について、前後左右それぞれの方向のグラフをくっつけたものです。
この場合Ｚというのはグリップ力の最大値ですね。
それに対していわゆる「摩擦円」というのは、ベクトルの考え方をもとにした図です。
普通の数式のグラフと、ベクトルをもとにした図、それぞれ考え方が違うので図が違うのは当たり前なのですが、あらためて言われてみると混同するのも無理はないかもしれません。

簡単に違いが分かる図を描きますと、







グリップ力の最大値はN（ニュートン）で表せばよいので仮にＺ＝1000Nとすると、数式のほうは1000N＝Ｘ＋Ｙとなります。
この数式を前後左右のグリップ力それぞれについてグラフにすると、確かにダイヤモンド型になります。
ところがベクトルで考える場合は1000Nというのが矢印の「長さ」になります。
摩擦円を真円と仮定する場合は「360度どの方向についてもグリップ力は同じである」という前提になりますので、矢印の長さが変わってはいけません。





縦に50％なら横に50％、というのはなるほど言葉としてはまさにそのとおりです。
ただし摩擦円の考え方に従いベクトルで考える場合、ナナメ45度のときの縦または横方向の成分は1000Nにsin45°（≒0.7）を乗じた値になりますので、500Nにはなりません。
違和感を持たれる方もいるかもしれませんが、ベクトルとはそういうものです。






縦方向のベクトル成分を左右ナナメ方向45度それぞれに分解した場合でも同じで、500Nにはなりません。
横方向でも同じですね。

前後左右のグリップ力を考えるときにＺ＝Ｘ＋Ｙというのはちょっと不適切かと思いますが、必ずしも「間違い」だとは言い切れないと思います。
もしも仮に「そっちのほうが分かりやすい」という方がいるなら、べつにそれでいいんです。
そういうことは重要じゃなくて、摩擦円が「ベクトルをもとにした図である」ということがきちんと説明されなかった、という事実が重要です。
要改善ですね。

ところがところがベクトルの説明など一切なかったしたら、数式をもとにして考えてしまう方がいても無理はないように思います。
そうだとすると、摩擦円を見たときに「なんかおかしいんじゃない？」と疑問を持つことも自然なことですよね。
この「なんかおかしいんじゃない？」というのはすごく大事なことで、この方は摩擦円についての事柄を「自分で考えることが出来ている」ということですね。
結果が重要なのではありません、自分で考えることが出来ているということが重要です。
素晴らしいですね！

　摩擦円は円である→本当か？
　バネは硬いほうがいい→本当か？
　バネが硬いのはよくない→本当か？
　トーコントロールをキャンセルするとスポーティになる→本当か？
　akiさんはお洒落でイケメンで大金持ちのエリートで歩いた足跡からお花が咲く→本当か？（笑）
　※最後のはうそです（笑）

僕もそうなんですけど基本的に多くの人は、「なるほど！」と思ったことがあると他人に話したくなるものです。
インターネットにはそのような記事が溢れています。
ところが皆さんご存知のように全てが正しいとは限らない。
世間で言われていることをきちんと疑うことが出来て、自分なりに検証し、そして主張としてまとめ上げることが出来る。
ダイヤモンド型グラフの記事を書かれた方の場合はあと一歩というところで惜しかったですね、でも大健闘だと思います^^
摩擦円が円であると疑いもしないことと、「なんかおかしいんじゃないか？」と疑えること。
違いは明らかですね。

と、いうわけで摩擦円のお話でした。
言っときますが僕がエライのではありません、この方がエライんです（笑）
あらかじめどの程度の知識を持っているかどうかはその人の本質には関わりのないことです。
自由な発想でいろいろと考えようとする気持ちが大事ですね^^

こないだアンチリフトのお話を書きました。
「クルマの姿勢を制御するものであって、タイヤへの荷重が減る/増えるのを抑えられるわけではない」
じゃあなんでステア特性が変わるんだ、って思われた方もいるかもしれません^^;

基本的にはロールセンタで考えればよいと思うのですが（リヤのロールセンタ上がる→ロールセンタと重心との距離が縮まる→リヤのロール剛性上がる→オーバーステア）、同時にロールステアの絡みがありますので、ついでなので書いときます。

まずこちらの適当なイラストを見て頂いて、







左がクルマを上から見た図、右がクルマを前から見た図ですけど、







クルマを上から見た図のうち、フロント左側のタイヤに注目したのがこの図で、






のちのち説明しやすいように線を細くして、色分けしたのがこの図です。
水色のアームをタイロッドとし、紺色のアームをロアアームとします。
タイロッドやロアアームが何か分からない方は残念ですが今日のお話は読み飛ばして下さい^^;






ところで、もし仮にですけど、ロアアームが短くなったとします。
タイロッドの長さはさっきと同じです。
すると、タイヤは外側を向きますね。
いいですよね、ロアアームが短くなるとタイヤは外側を向きます^^






次にこちらの図ですけど、クルマを前から見た図です。
都合上、タイロッドとロアアームを上下にズラして描画していますが、同じ高さにあるものとして考えてください。
ホントはナナメからの視点で図を描けたら分かりやすかったんですけど…。
すいません、そんな器用なこと出来ないので^^;

この図では、タイロッドよりもロアアームのほうが短いです。
薄いグレーになっている幅の分だけ短くなっていますね。
しかしこういう取付状態であれば、タイヤはまっすぐボディと並行です。
タイヤはまだ外側を向いていません、いいですよね。





さて、このタイヤが上下に動くとき、タイロッドとロアアームはメンバー側取付点を中心として円軌道で動きます。
水色の矢印がタイロッドの、紺色の矢印がロアアームの軌道を表しています。
ロアアームのほうがタイロッドより短いので、ロアアームが描く円はタイロッドが描く円よりも小さいです。
したがって軌道が「より内側」にきますね。






「このへん」に注目してみると分かりやすいですね。
ずいぶんと差があります。
この差が重要です。

このような配置になっているサスペンションがあったとして、タイヤが上方向に動いたとすると、どうなるでしょうか？







こうなります。
なんと、タイヤが外側を向きました！^^

赤色のアッパーアームと水色のタイロッドは、長さが同じ。
それに対して、紺色のロアアームは長さが短いです。
そのためタイヤが上方向に動くと、ロアアームのところだけ「内側に」引っ張られます。
変な言い方かもしれませんが、ロアアームが短くなったのと同じようなものです。

いまいち納得できない方のためにおさらいしますと、






まず円軌道で動く２本のリンクがあったとして、もしもこの２本のリンクが同じ長さだったら、






上下方向に動いたときにも、






動き方は同じです。
円軌道で動くので先端は少し内側に移動しますが、その移動する量も同じです。






ところが２本のリンクの長さが違う場合、






上下に同じ量だけ動いたとき、先端が内側に移動する量が異なります。
円の小さいほうが、「より内側に動く」ことになります。
わかりますよね^^

この理屈を利用して、サスペンションはタイヤのトー角をコントロールしています。
サスペンションが何cm縮んだときは、トー角が何℃変わる、みたいな感じです。
今回の例ではアームが地面と並行でしたが、地面と並行でないように作ると、縮み側と伸び側でトー角の変化の具合も変えることができます。
興味が出た方は図を書いて、「こんな変化のさせ方はできないかな～」といろいろ考えてみてください^^

で、たいていの市販車のリヤサスペンションの場合、基本的にはですけど、縮み側でトーインです。
だから車高短にするとリヤはトーインです。
ところが車高短の状態でアライメントを取ってトーゼロにすると、今度はサスペンションが伸びたときにトーアウト方向に向きます。
さらにもっともっと伸びればトーゼロを経て再びトーイン側に戻るかもしれませんが…どれくらい伸びればトーインに戻るかは…車種や車高によりますね^^;

というわけで、ブレーキでリヤが浮き上がるとこういう変化もあるんだよ、というお話でした。
当然ですけどキャンバも減りますし、実はそれ以外にも…。

クルマって難しいですね、わけわからんです^^;