■ナビゲーション

2011年01月05日

容疑者Aの本能 ≡ 数学者Bの挑戦（mod盗難車Xのメッセージ）　　　（PC）

まずはじめに、2010年度、盗難車ワースト10は以下通りです。。。

1位

ハイエース

2位

ランドクルーザー

３位

セルシオ

4位

ワゴンR

５位

クラウン

6位

マークX

7位

タント

8位

キャンター

9位

ステップワゴン

10位

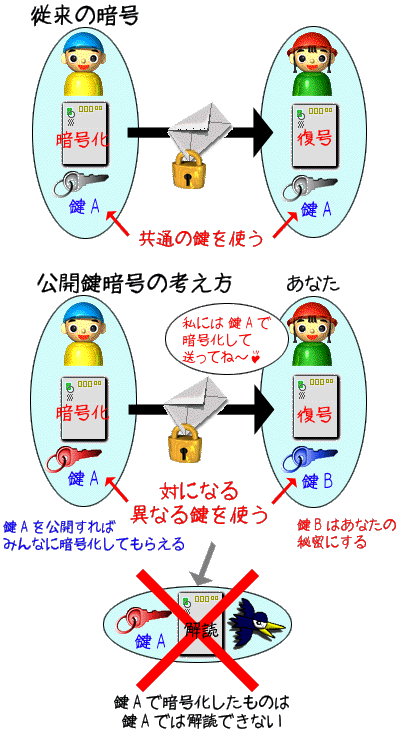
インプレッサ

車種からお分かりの通り、盗難車の多くはドバイを経由して、アフリカなどに流れてるそうです。
セキュリティ技術が発達した現在も尚、車の盗難件数は減るどころか増える一方です（≧≦）

ＲＳＡ暗号は、インターネットセキュリティやカーセキュリティでも広く利用されている話題の暗号です。この暗号をはじめとする現代の暗号は、戦争中に一部組織でのみ使用されてきた暗号とは全く異なり、情報セキュリティを確保する根幹技術として、情報ネットワーク社会に生きる我々に大きな安心を与えてくれるものです。ともすれば、既に無意識のうちに利用されている方もいるでしょうし、少なくともこれからの生活には必要不可欠なものとなるでしょう。

このような現代暗号には、ＲＳＡ暗号の他にもＤＥＳ（デス，ディ・イー・エス）やＡＥＳ（エー・イー・エス）など、非常に数多くの方式が存在します。多くの暗号が複雑な設計であるのに対し、現代暗号の中で最も特徴的なＲＳＡ暗号のエッセンスはとっても単純かつ面白い理論によって成り立っています。

僕が今回気になったのは、暗号の方式ではなく、暗号の「からくり」の方です。

ということで、普段何気なく使用していの暗号のカラクリを、ある優秀な大学生の書き物を読んで勉強してみました。

ＲＳＡ暗号ではある数を法（モジュロ）とする世界で、平文の数値を別の数値に変換します。ＲＳＡ暗号を支えるこの世界の数値の興味深い性質をお話しします。

ＲＳＡ暗号は、自由に選んだ異なる二つの素数を掛けた数を法とする世界を利用します。素数というのは、例えば、2, 3, 5, 7, 11, ... のように、その数自身と 1 以外の自然数では割りきることができない 2 以上の整数のことです。 4 は 2 で、 6 は 2 や 3 で割りきることができるから素数ではありません。では、そのような世界の例として、二つの素数に 3 と 11 を選び、これらを掛けた数 33 を法とする世界を考えてみましょう。 33 を法とする世界に存在する数は、0 から 32 までだけです（ 33 までいったら 0 に戻るからです）。

この世界に存在する全ての数のべき乗を全て求めて表にしてみます。

これは、ある数値の○乗はいくつか？という表です。一番左の列がべき乗されるこの世界の数、一番上の行が何乗するかという数です。例えば、べき乗される数が 2 の時は、 1 乗で 2、 2 乗で 4、 3 乗で 8、 4 乗で 16、 5 乗で 32、 6 乗で 64 … 64 は 33 を法とする世界では 31 になります。そしてまた、 6 乗で 62 … 62 は 33 を法とする世界では 29 … という風に続けていきます。

さて、この表をよく見て下さい。 33 を法とする世界に存在する 1 から 32 までの全ての数は、べき乗する度に予想のつかない数に変わっていきながらも、全ての数はなんと11 乗又は 21 乗すると自分自身に戻っているでしょう！（水色のセルの部分）このように、２つの素数（ P, Q とします）をかけた数を法とする世界では、全ての数が自分自身に戻るべき乗数が必ず存在します。そして、これが何乗なのかは、最初の２つの素数 ( P , Q ) によって決まります。つまり、実はその２つの素数さえ分かってさえいれば、このべき乗数は簡単に求めることができるのです。

それは、P と Q からそれぞれ 1 を引いた P-1 と Q-1 の最小公倍数に 1 を足した数です。すべての数は、この数の回数だけべき乗した時、必ずもとの数に戻るのです。そして、そのようになるべき乗数は、一定のペースでまたやってきます。そのペースとは、 P-1 と Q-1 の最小公倍数です。従って、P×Q を法とする世界で、全ての数が自分自身に戻るべき乗数は、n × （ P-1 と Q-1 の最小公倍数）+ 1と表すことができます。ちなみに (P-1)×(Q-1) という式は必ず（ P-1 と Q-1 の最小公倍数）の倍数になりますので、このべき乗数の一部は簡単に

n × (P - 1) × (Q - 1) + 1

（但し n は任意の正の整数）
として求めることができます。

どうでしょう、先程の２つの素数 P=3, Q=11 とする時、 P-1=2 と Q-1=10 の最小公倍数は 10 であり、n × （ P-1 と Q-1 の最小公倍数）+ 1 は n=1 で 1×10 + 1 = 11 となりますが、確かに上記の表を見てみると 11 乗でどの数も必ず自分自身に戻っています！また、n×(P-1)×(Q-1) + 1も、 n=1 で 1×(3-1)×(11-1) + 1 = 2×10 + 1 = 21 となり、上記の表と同じく、 21 乗でも同様のことが起こっているのが分かります。
　
さぁ、これをどう暗号化に利用するのでしょうか？気が付きますか？ＲＳＡ暗号では、このように適当な素数 P , Q を掛けた数 P×Q を法とする世界を考え、暗号化したい平文の数値（但し P×Q 未満）を、「適当な数」分だけべき乗してしまうのです。ここで何乗するかというのが１つ目の鍵(E) となります。すると、あらゆる数は予想がつかない数に変換されます。これが暗号化でこれにより変換された数値が暗号文（暗号語）となるのです。そして、この暗号化された数値をもとの数値に戻す復号を行なうには、暗号化の際べき乗した数（ E乗）の部分から、全体として自分自身に戻るようなべき乗数になるようさらにべき乗してやればよいのです。このべき乗数が鍵 (E) に対応するもう一つの鍵 (D) となるのです。

ここで「わざわざ (D) 乗しなくても単に (E) 乗根を求めれば元の数が得られるのでは？」という疑問を持たれる人もいるかもしれません。それは確かに私たちが住んでいる普通の世界なら可能です。例えば 2 を 4 乗して 16 を得た時、 16 の 4 乗根を求めれば元の 2 が得られます。しかし、今、この暗号で利用している素数を二つかけ合わせた数を法とする世界は我々の世界のような単純な割算はできないため、逆に（ E乗）分を逆算して元の数に戻すことができないのです。これが暗号化に使用した鍵では復号ができない「からくり」になっているのです。

いかがでしょうか？ＲＳＡ暗号のからくりが、なんとなく分かってきましたか？まだわかっていなくても、大丈夫。次でもう一度具体的に解説しますから。

では実際に、自由に選んだ２つの素数の例に P=3, Q=11 を選び、それらを掛けた P×Q = 33 を法とする世界を利用して、ＲＳＡ暗号による暗号化を行ってみます。

相手に秘密に伝えたい平文の数値列を、7 13 17 24 とでもします（実際に文字を暗号化する時は、一旦文字を数値に直すのです）。これを友人から自分に送ってもらうことを想定します。まず、暗号化するための鍵（公開鍵暗号方式の概念を覚えていますか？暗号化するための鍵はみんなに公開してしまうのです）を決めます。すなわち、 33 を法とする世界で暗号化の際に一旦何乗するかということです。

では、この公開する鍵を適当に 3 に決めましょう（但し、実際は適当にはとれず多少の制限があります）。そしてこれを友人に伝えます。" 33 を法として、鍵を 3 として暗号化してくれ"と。よって公開する情報は、法とする数 33 と公開鍵 3 です。友人は平文 7 13 17 24 を言われた通りの条件で暗号化します。 33 を法とする世界でのべき乗表をもう一度下記に示しておきますので、参考にしてください。

まず 7 は、 3乗すると 13。
次、 13 は、 3乗すると 19。
次、 17 は、 3乗すると 29。
最後 24 は、 3乗すると 30。
従って、平文 7 13 17 24 の暗号文は 13 19 29 30 となります。

さて、この暗号文を受け取ったあなたはこれを復号して平文に戻します。それには、公開した鍵 3 のペアとなる秘密の鍵を求めて、さらにその数分だけ暗号文をべき乗してやればよいはずです。 33 を法とする時、存在する全ての数は n×(3-1)×(11-1) + 1 乗すると元に戻るのですから、 3 という鍵で暗号化したなら（既に 3 乗されているので）、3 乗した時の数をさらにある数 (D) 乗した結果が、全体として n×(3-1)×(11-1) + 1 乗（n は任意の整数）になるようにすればいいのです。分かりますか？

A を平文の数値とする時、暗号化に使った鍵が 3 なので A を暗号化した後の値はすでに 3 乗されているため、全体として A が再び元の A に戻るだけのべき乗にしてしまうような秘密の鍵 D は、

(A3)D = A{n × (P - 1) × (Q - 1) + 1}

という関係がなければならないので（但し n は自由な正の数）、

3 × D = n × (P - 1) × (Q - 1) + 1
↓
3 × D = n × (3 - 1) × (11 - 1) + 1
↓
D = 3分の n × 2 × 10 + 1

という式を満たす必要があります。このような D としては… n が 1 の時にD=7となりますから、この 7 が暗号化の鍵 (E) として 3 を使った暗号文を復号できる秘密の鍵 (D) となります。では求めた秘密の鍵 7 で送られてきた暗号文 13 19 29 30 を復号してみましょう。 33 を法とする世界で考えるんでしたね。

まず 13 は、7 乗すると 7 。
次、 19 は、7 乗すると 13。
次、 29 は、7 乗すると 17。
最後 30 は、7 乗すると 24。
結果、7 13 17 24 となり、最初の平文に一致します。見事に復号することができました。

ＲＳＡ暗号の暗号化と復号の手順が分かりました。少しだけまとめると、まず自由な２つの異なる素数 P , Q を定め、 N ( = P×Q ) を法とする世界を考えるのです。この P×Q を法とする世界で、平文の数値を適当に定めた E 乗することで暗号化を行ないます。この時、全ての数は n×(P-1)×(Q-1) + 1 乗するとどんな数も必ず自分自身に戻るため、

(AE)D = A{n × (P - 1) × (Q - 1) + 1}

という関係がなければならないので（但し n は自由な正の数）、

E × D = n × (P - 1) × (Q - 1) + 1
↓
D = E分の n × (P - 1) × (Q - 1) + 1

（専門書では「逆元」と「ユークリッドの互除法」により同式を得ます）
から D を求め、暗号化した数値を D 乗すれば、ふたたび元の平文の数値に戻ることになるはずです。従って、この D が、E 乗して暗号化した暗号文を復号できる鍵になります（但し E は (P-1)×(Q-1) と互いに素な数とする必要があります）。

結局、重要なのは２つの素数P と Qです。法とする数 P×Q と、暗号化に使う鍵 E は公開してしまうので、もしも P と Q がバレてしまったら秘密にしなければならない鍵 D を上の式から求められてしまいます。 P と Q は暗号としては２つの鍵を作り出すのに必要なだけで、直接暗号化や復号の作業には登場しないものなので、一度鍵を作ったら P と Q をメモした紙は食べてしまうくらいな方が一番よいかもしれません。

しかし、このような仕組みでは、ある疑問がわきませんか？「 P×Q の結果は公に教えてしまうのに P と Q 自体は教えてはいけない」なんて…でも「P×Q を教えたら P と Q が分かってしまうのではないのか？」と。つまり、先ほどの例で言えば「ある素数と素数を掛けたら 10 になった（ P×Q = 10 ）」ということは教えるけども、つまり「それがいくつといくつか（ P=2, Q=5 ）」は教えてはいけないなんて、 P×Q = 10 が分かれば、誰でも P=2, Q=5 って分かっちゃうんじゃじゃないの…？ということです。

それがＲＳＡ暗号の重要なミソのなのです。これ、素因数分解の事ですよね。

「素因数分解」は、中学生三年生で習うはずです。ある数が与えられたら、その数と 1 でしか割りきることができない 2 以上の整数…すなわち素数を使った掛け算の式に分解することです。例えば、 33 なら 3×11 という式に分解できますね。 3 も 11 もそれぞれ素数ですよね。

あらま！?、そんな方法があるのなら、法とする数 P×Q = 33 を公開してしまえば、誰にでも P=3, Q=11 であることが分かってしまいまいますョ…。そして公開する鍵 E は公開されてるから秘密の鍵 D を求められてしまいます。う～ん、これは困りましたね…。でもこの 33 の素因数分解、あなたはどのような方法で 3×11 に分解できることが分かったのですか？

実はこれ、人間の勘と長年の経験によるところが非常に大きいのです。その証拠に、それでは6887はどう素因数分解されますか？これも２つの素数に分解できるのですが、一体どうしたら分解できるかなんて数学者でもきっと思い付かないでしょう。思い付いたとして、きっと2 から順に 3, 5 ...って割れないかどうか順に試してみるくらいがオチじゃないですか？

それもそのはず、なんと現在のところ巨大な二つの素数を掛け合わせた数を素因数分解する効率的な方法が見つかっていないのです…。つまり二つの素数 P=3 と Q=11 を掛けて P×Q = 3×11 = 33 を求めることは簡単にできますが、逆に掛けた結果の P×Q = 33 から P と Q ( 3 と 11 ) を知ることは極めて難しいのです。これが重要なのです。 6887 を素因数分解できなかったのは、決して僕の頭が悪かったからではないのです。ちなみにこれは 71 と 97 に素因数分解できます。実際に掛けてみて下さい、71 と 97 を掛けて 6887 を求める方は小学生でも出来ますから。

先ほどのＲＳＡ暗号は試しに P=3, Q=11 で P×Q = 33 という小さな数で行ったために P×Q = 33 から P=3 と Q=11 を割り出せてしまいましたが、これが巨大な素数を掛けたものとなると決して割り出せなくなってしまうのです。この結果、法とする数 ( P×Q ）と公開鍵 E を公開してしまっても、 P, Q を使って秘密鍵 D を求めた本人以外に、秘密鍵 D を知られずに済むのです。ＲＳＡ暗号は、暗号のしくみは「奇跡が起きるべき乗数」に、そして安全性はこの素因数分解の難しさによって保証されているのです。

暗号解読の前に数学って面白いですね＾＾
その面白いという心を正義の為に使って欲しいのですが、数学者や科学者または物理学者は、発明した後の、使う人間のことまでは考えてくれませんよね。。。

PS
タイトルの容疑者Aの本能 ≡ 数学者Bの挑戦（mod盗難車Xのメッセージ）とは、以下の通りです。
a, b, m を整数とする。
a と b を m で割った余りが等しい時、a と b は m を法として合同であるといい、
a ≡ b ( mod m ) と書きます。
例 )
5 ≡ 2 ( mod 3 )
8 ≡ 18 ( mod 2 )
14 ≡ 0 ( mod 14 )
-7 ≡ 19 ( mod 13 ) 等。

ブログ一覧 | 気になって仕方ないこと | クルマ
Posted at 2011/01/05 06:14:36

<< たまには。。。

| 記事一覧 |

なんなんだこの人は。。。（ ... >>

イイね！0件

イイね！ランキングページへ

今、あなたにおすすめ

ブログ人気記事

前線消滅！時間無いCCWGPブース ...
NTV41chさん

怪しいバス乗車
KP47さん

真上から撮影
wakasagi29_さん

8/16 土曜日の朝‼️
ミッキーたんさん

200万円弱で買えるカババアウデ ...
ひで777 B5さん

朝の一杯　8/15
とも ucf31さん

この記事へのコメント

コメントする

angel♂(ニート) 2011年1月5日 6:27 おはようございます（＾Ｏ＾☆♪ 頭から煙りが出てきました(^◇^;)	コメントへの返答 2011年1月5日 6:34 おはようございます♪ 僕も理解するまでに何度も読み返しました（≧≦）
さんき 2011年1月5日 7:25 さてと。。。ウンコしてくるわ＊＾＾＊	コメントへの返答 2011年1月5日 7:29 まだ頭が回転するには時間が早過ぎたね（´〇｀；）今日も寒いから気をつけてねぇ♪
O.i.r.a.123。 2011年1月5日 7:37 悪のテクノロジーは侮れない。法やセキュリティが進化したらそれ以上に進化する。中途半端は悪人にもなれない。	コメントへの返答 2011年1月5日 8:31 悪の手に渡るか、善の手に渡るかですが、感情がある人間ですからどちらの手に渡っても≡（合同）ということにもなりますよね…orz
Donfan 2011年1月5日 8:41 今頃ですが新年おめでとうさんです。今年もヨロシクね☆ １０年程前に１６アリスト盗まれたのを思い出しました。新車から１０ヶ月で海外に持って行かれましたが、その後約一年半程してから犯人検挙の連絡がありまし。既に保険屋さんへ委任状を出していましたので僕には関係なかったですが、室内に置いてた物品とかトランクのゴルフクラブとか返して欲しかったなぁ～（泣）	コメントへの返答 2011年1月5日 8:48 こちらこそ、改めまして新年明けましておめでとうございます！今年も宜しくです＾＾悪い記憶を呼び起こしてしまい、申し訳ないです（≧≦）愛車を盗まれるなんて、考えただけでゾッとします。。。お怪我がなかっただけでも良かったですね！ですが、このような悲しい結果を招かない為にも、セキュリティの強化にやり過ぎという言葉はありませんね！
せなっち＠書記長 2011年1月5日 8:42 脳が膿みました・・・・(＠_＠;)	コメントへの返答 2011年1月5日 8:50 僕も書きながら、あれっ?ここってどうやってたっけ?と何度も手が止まりましたｗｗｗ理解したら、暗号の世界って面白いでしょ♪
八百屋＠兼業農家 2011年1月5日 9:10 なんで戻るの？？超こえぇ（爆）こういうのおもろいよねぇｗ	コメントへの返答 2011年1月5日 9:15 それが素因数分解を使用した暗号解読の難解なところでもあり、面白いところです＾＾はい、僕も久々に勉強になりました！
スタッキー 2011年1月5日 9:14 いま正常にｺﾒﾝﾄしておりますが途中からの記憶がありません（爆）ww しかし盗難車のﾜｰｽﾄの中にﾜｺﾞﾝRやﾀﾝﾄが含まれているのには驚きました...汗）	コメントへの返答 2011年1月5日 9:18 この時間に真面目に読む方はいないと思いましたが、昨日ＵＰ出来なかったので、頭フル回転で書きましたｗｗｗ見て頂いただけでも感謝です♪ 僕も驚きました！もっと高級車ばかりだと思ってました（＾＾；）
rouge40 2011年1月5日 10:17 おはようございます。こういう本を夜中に読んでるってとこがスゴイです。途中まで読みましたが挫折しました。すみません。盗難車ランキングはタマ数とか、海外での需要とかが関係あると思うのですが、 TOYOTA車多いですね。（ヤバ）でもレクサスを盗むツワモノも存在するんでしょうね。究極の盗難対策はハンドル外すとかかな。	コメントへの返答 2011年1月5日 10:36 おはようございます＾＾気になったら、調べないと落ち着かなくて(^_^;) いえ、例え数学者でも1回スラスラっと読んだだけでは、理解できないと思いますから大丈夫ですよ♪ 筆者の教え通り、僕も何回か計算しながら読返すと理解できました。確かに完全に盗まれないようにするには、おっしゃる通りハンドル外すか、ホイール外すとか、物理的に動かせないようにするしかないですよね（≧≦）
レクサス守・高 2011年1月5日 10:58 こんにちは。ムッチャ難しいです。こんなんいたちごっこで、永遠の課題ですよね。	コメントへの返答 2011年1月5日 11:41 こんにちわ＾＾すいません、もっと噛み砕いて書けば良かったですかね(^_^;) はい、解けない暗号なんてありませんから、永遠にイタチゴッコです。。
風神＠あひる隊長 2011年1月5日 11:28 それでも盗む側は、解析してしまう・・・奴等も必死です。。。結局のところ、物理的なセキュリティーが一番効果があるようです。（地面に車体を固定してしまう等・・・w）盗難で多いのが、キー付けっぱなし（コンビニ等）らしいですし・・・w	コメントへの返答 2011年1月5日 11:48 その解析してしまう頭脳を、医療の分野で発揮してほしいものですよね（≧≦）おっしゃる通りですね。物理的アプローチが一番美しい形というか安全ですね☆ ゆえに、物理と数学の大きな違いがここにありますね！コンビニにキー付けっぱなし…GSはよく、エンジンかけたままコンビニに入りますwww
フェローズ 2011年1月5日 12:14 ほんとだ戻る…不思議だなぁ！勉強になるわ！度忘れしたんだけど、最大公倍数ってどうやって求めてたっけ？	コメントへの返答 2011年1月5日 12:22 俺も改めて、素因数分解の難易度を思い知らされた。。。逆さ割算すれば簡単だよ。出た約数を、縦横とも全部掛けた答えが最大公倍数。ちなみに最大公約数は、同じ逆さ割算で縦だけ掛けた答え。学生時代に分数で習ったから懐かしいよな＾＾補足割る数は全て素数じゃないとダメだよ。
シャンクス（石川） 2011年1月5日 12:27 さ・さ・さっぱり分からん…(--;) １番苦手な分野です(+_+) １番得意な分野は、女とS○Xです(ﾟзﾟ)ﾌﾟｯ！それにしても、盗難車ランキングに軽が入ってくるなんて、意外ですね(^_^;) レクサスが入ってなくてよかった(^皿^)	コメントへの返答 2011年1月5日 19:40 僕も苦手な分野で、同じく得意なのは生物系です(^_^) 軽の完成度の高さがうかがえますよね！ですが軽は、物理的セキリュティ面ではノーガードに近いですからね（≧≦）
SAM1959 2011年1月5日 13:45 脳が腐りました（笑）盗難に関しては3位に浮上した３系セルシオはトヨタ車のイモビの欠点を突いた方法が使用出来るとの情報が出回ったので急激に増えたと噂されてます。イモビの暗号を破る方法ではないので暗号意味無しです(;^;) 同じイモビ方式を使っていたトヨタ車は社外盗難防止付けないと狙われたらおしまいです	コメントへの返答 2011年1月5日 19:43 僕も最初頭痛くなりました（_）セルシオのイモビは有名な話ですよね！やはり最終的には、自分の身は自分で守らなきゃイケないんですかね。。
じうーこ 2011年1月5日 15:04 こんにちは♪Lさん！何となく分かった様な分からない様な・・・良くこんな文章かけるね！頭良い証拠だわ！おっちゃんちょっと眠くなって来た。。。様はセキュリティは万全にしろと言う事ですね♪	コメントへの返答 2011年1月5日 19:45 じうーこさん、こんばんわ＾＾大学の優秀な研究員さんのお陰ですよ！僕は何度も読返して理解しましたから、頭良くないですよ（≧≦）はい、お互い気をつけましょうね♪
彩葉 2011年1月5日 15:28 数字苦手なので　ヽ(+∇+)ノ・・・キュゥ　状態ですセキュリティ対策をしても、被害に遭う方がいらっしゃる。本当に腹立たしいですヾ(o｀皿´o)ノ＠)) 暮れにセルシオの盗難が増えているという記事を読みましたが、やっぱりハイエースなんですね(；´ω｀)ﾀﾗｰﾘ･･･	コメントへの返答 2011年1月5日 19:49 僕も理解するまでに、頭ショートしそうになりました。。。人の気持ちがどれだけ傷付くのか、分からないんでしょうね（≧≦）ハイエースは海外でも大人気みたいですね。日本車はガソリン車も、ディーゼル車も、20万km以上走っても、ノントラブルですもん！
匠~TAKUMI~ 2011年1月5日 18:17 理系大卒なんですが途中から理解するのを諦めました(汗)	コメントへの返答 2011年1月5日 19:52 お忙しい中、長文すいません（≧≦）理系かじってらっしゃいますし、僕より早く理解できるて思いますよ＾＾僕は時間かかりましたから。。
ドン・コルレオーネ 2011年1月5日 18:31 お邪魔しました（爆）過去に所有していたセルシオ（３０後期）も、イモビを解読され同モデルの盗難が多発しているそうです。窃盗団も”イモビカッター”を使い瞬時に持ち去る手口・・・まぁ時間の問題だと思ってましたが(>_<) と、こんなもんで如何でしょうか"^_^" 今夜、、、夢●しそうです（謎爆）	コメントへの返答 2011年1月5日 19:55 ウケましたwww 1度解読されてしまうと、簡単に持ち去られてしまいますから、やはり物理的セキリュティが必要になってきますよね（≧≦）楽しい夜になりそうですね(￣―＋￣)
せきとり 2011年1月5日 19:35 食いもんの話ちゃうのん？ (´0`)ふぁ~	コメントへの返答 2011年1月5日 19:56 どう連想したら食いもんの話になるんすかwww
ＨＩＳＡ 2011年1月7日 6:23 途中で頭から煙がモクモクでてきましたｗｗこういう難しい話はＰＣの画面より紙の方が見やすいですね！	コメントへの返答 2011年1月7日 9:08 分かりにくい書き方しちゃったね（≧≦）確かにwww 項目別に頁分けたら見やすかったんだけど、ひとつにまとめちゃった(^_^;)
フェローズ 2011年1月7日 9:51 やっと解けたよ（汗）てかほんとこの素因数分解ってほんと不思議よね。暗号鍵と複合鍵、文章と計算式ずっと睨めっこしてたから頭痛いわ！	コメントへの返答 2011年1月7日 10:11 おめでとう♪ 俺もすぐに解けなかったよ(^_^;) 4桁になると、いきなり素因数分解は難しくなるよね。今日は数字見ないで仕事しなさいwww て仕事柄無理か。。。

<< たまには。。。

| 記事一覧 |

なんなんだこの人は。。。（ ... >>

プロフィール

「祝・みんカラ歴17年！ http://cvw.jp/b/333720/48070336/」

何シテル？ 11/06 07:53

Ｌ-ＦＩＮＥＳＳＥ

沈黙を美徳とし、多くを理解しながらも、やわらかな表現で、言葉の奥底にあるものを伝える日本人。この日本的な考えや文化、歴史が、レクサスのデザインフィロソフィー...

ユーザー内検索

<< 2025/8 >>

リンク・クリップ

Google Android Auto カテゴリ：その他（カテゴリ未設定） 2023/04/22 14:28:56
備忘録、 TT第4回目オイル交換カテゴリ：その他（カテゴリ未設定） 2023/04/21 18:06:56
不明大陸製ルーフレールカテゴリ：その他（カテゴリ未設定） 2023/04/18 08:27:17

[ 他のクリップをチェック ]

愛車一覧

	アウディ Q2 21年モデルにMCしたらTTから乗り換えで購入したいと思います。 A1からの乗換で当初は ...
	アウディ R8 （クーペ）やはり普段乗る分にも快適に速いAudi技術の結晶年式 : 2021年式グレード : ...
	アウディ A1 スポーツバック街乗り専用車🚘✨✨✨ 2023年7月にQ2君と入替です🚘🚘
	アウディ R8 （クーペ）街乗からサーキットまで優雅に熟すAudi技術の結晶 2日間お借りして、スーパーカーとし ...

[ 愛車一覧 ]

過去のブログ

2024年
01月	02月	03月	04月	05月	06月
07月	08月	09月	10月	11月	12月
2023年
01月	02月	03月	04月	05月	06月
07月	08月	09月	10月	11月	12月
2022年
01月	02月	03月	04月	05月	06月
07月	08月	09月	10月	11月	12月
2020年
01月	02月	03月	04月	05月	06月
07月	08月	09月	10月	11月	12月
2019年
01月	02月	03月	04月	05月	06月
07月	08月	09月	10月	11月	12月
2018年
01月	02月	03月	04月	05月	06月
07月	08月	09月	10月	11月	12月
2011年
01月	02月	03月	04月	05月	06月
07月	08月	09月	10月	11月	12月
2010年
01月	02月	03月	04月	05月	06月
07月	08月	09月	10月	11月	12月
2009年
01月	02月	03月	04月	05月	06月
07月	08月	09月	10月	11月	12月
2008年
01月	02月	03月	04月	05月	06月
07月	08月	09月	10月	11月	12月
2007年
01月	02月	03月	04月	05月	06月
07月	08月	09月	10月	11月	12月

RSS2.0

ヘルプ｜利用規約｜サイトマップ

あなたの愛車、今いくら？

複数社の査定額を比較して愛車の最高額を調べよう！

angel♂(ニート) 2011年1月5日 6:27 おはようございます（＾Ｏ＾☆♪ 頭から煙りが出てきました(^◇^;)	コメントへの返答 2011年1月5日 6:34 おはようございます♪ 僕も理解するまでに何度も読み返しました（≧≦）
さんき 2011年1月5日 7:25 さてと。。。ウンコしてくるわ＊＾＾＊	コメントへの返答 2011年1月5日 7:29 まだ頭が回転するには時間が早過ぎたね（´〇｀；）今日も寒いから気をつけてねぇ♪
O.i.r.a.123。 2011年1月5日 7:37 悪のテクノロジーは侮れない。法やセキュリティが進化したらそれ以上に進化する。中途半端は悪人にもなれない。	コメントへの返答 2011年1月5日 8:31 悪の手に渡るか、善の手に渡るかですが、感情がある人間ですからどちらの手に渡っても≡（合同）ということにもなりますよね…orz
Donfan 2011年1月5日 8:41 今頃ですが新年おめでとうさんです。今年もヨロシクね☆ １０年程前に１６アリスト盗まれたのを思い出しました。新車から１０ヶ月で海外に持って行かれましたが、その後約一年半程してから犯人検挙の連絡がありまし。既に保険屋さんへ委任状を出していましたので僕には関係なかったですが、室内に置いてた物品とかトランクのゴルフクラブとか返して欲しかったなぁ～（泣）	コメントへの返答 2011年1月5日 8:48 こちらこそ、改めまして新年明けましておめでとうございます！今年も宜しくです＾＾悪い記憶を呼び起こしてしまい、申し訳ないです（≧≦）愛車を盗まれるなんて、考えただけでゾッとします。。。お怪我がなかっただけでも良かったですね！ですが、このような悲しい結果を招かない為にも、セキュリティの強化にやり過ぎという言葉はありませんね！
せなっち＠書記長 2011年1月5日 8:42 脳が膿みました・・・・(＠_＠;)	コメントへの返答 2011年1月5日 8:50 僕も書きながら、あれっ?ここってどうやってたっけ?と何度も手が止まりましたｗｗｗ理解したら、暗号の世界って面白いでしょ♪
八百屋＠兼業農家 2011年1月5日 9:10 なんで戻るの？？超こえぇ（爆）こういうのおもろいよねぇｗ	コメントへの返答 2011年1月5日 9:15 それが素因数分解を使用した暗号解読の難解なところでもあり、面白いところです＾＾はい、僕も久々に勉強になりました！
スタッキー 2011年1月5日 9:14 いま正常にｺﾒﾝﾄしておりますが途中からの記憶がありません（爆）ww しかし盗難車のﾜｰｽﾄの中にﾜｺﾞﾝRやﾀﾝﾄが含まれているのには驚きました...汗）	コメントへの返答 2011年1月5日 9:18 この時間に真面目に読む方はいないと思いましたが、昨日ＵＰ出来なかったので、頭フル回転で書きましたｗｗｗ見て頂いただけでも感謝です♪ 僕も驚きました！もっと高級車ばかりだと思ってました（＾＾；）
rouge40 2011年1月5日 10:17 おはようございます。こういう本を夜中に読んでるってとこがスゴイです。途中まで読みましたが挫折しました。すみません。盗難車ランキングはタマ数とか、海外での需要とかが関係あると思うのですが、 TOYOTA車多いですね。（ヤバ）でもレクサスを盗むツワモノも存在するんでしょうね。究極の盗難対策はハンドル外すとかかな。	コメントへの返答 2011年1月5日 10:36 おはようございます＾＾気になったら、調べないと落ち着かなくて(^_^;) いえ、例え数学者でも1回スラスラっと読んだだけでは、理解できないと思いますから大丈夫ですよ♪ 筆者の教え通り、僕も何回か計算しながら読返すと理解できました。確かに完全に盗まれないようにするには、おっしゃる通りハンドル外すか、ホイール外すとか、物理的に動かせないようにするしかないですよね（≧≦）
レクサス守・高 2011年1月5日 10:58 こんにちは。ムッチャ難しいです。こんなんいたちごっこで、永遠の課題ですよね。	コメントへの返答 2011年1月5日 11:41 こんにちわ＾＾すいません、もっと噛み砕いて書けば良かったですかね(^_^;) はい、解けない暗号なんてありませんから、永遠にイタチゴッコです。。
風神＠あひる隊長 2011年1月5日 11:28 それでも盗む側は、解析してしまう・・・奴等も必死です。。。結局のところ、物理的なセキュリティーが一番効果があるようです。（地面に車体を固定してしまう等・・・w）盗難で多いのが、キー付けっぱなし（コンビニ等）らしいですし・・・w	コメントへの返答 2011年1月5日 11:48 その解析してしまう頭脳を、医療の分野で発揮してほしいものですよね（≧≦）おっしゃる通りですね。物理的アプローチが一番美しい形というか安全ですね☆ ゆえに、物理と数学の大きな違いがここにありますね！コンビニにキー付けっぱなし…GSはよく、エンジンかけたままコンビニに入りますwww
フェローズ 2011年1月5日 12:14 ほんとだ戻る…不思議だなぁ！勉強になるわ！度忘れしたんだけど、最大公倍数ってどうやって求めてたっけ？	コメントへの返答 2011年1月5日 12:22 俺も改めて、素因数分解の難易度を思い知らされた。。。逆さ割算すれば簡単だよ。出た約数を、縦横とも全部掛けた答えが最大公倍数。ちなみに最大公約数は、同じ逆さ割算で縦だけ掛けた答え。学生時代に分数で習ったから懐かしいよな＾＾補足割る数は全て素数じゃないとダメだよ。
シャンクス（石川） 2011年1月5日 12:27 さ・さ・さっぱり分からん…(--;) １番苦手な分野です(+_+) １番得意な分野は、女とS○Xです(ﾟзﾟ)ﾌﾟｯ！それにしても、盗難車ランキングに軽が入ってくるなんて、意外ですね(^_^;) レクサスが入ってなくてよかった(^皿^)	コメントへの返答 2011年1月5日 19:40 僕も苦手な分野で、同じく得意なのは生物系です(^_^) 軽の完成度の高さがうかがえますよね！ですが軽は、物理的セキリュティ面ではノーガードに近いですからね（≧≦）
SAM1959 2011年1月5日 13:45 脳が腐りました（笑）盗難に関しては3位に浮上した３系セルシオはトヨタ車のイモビの欠点を突いた方法が使用出来るとの情報が出回ったので急激に増えたと噂されてます。イモビの暗号を破る方法ではないので暗号意味無しです(;^;) 同じイモビ方式を使っていたトヨタ車は社外盗難防止付けないと狙われたらおしまいです	コメントへの返答 2011年1月5日 19:43 僕も最初頭痛くなりました（_）セルシオのイモビは有名な話ですよね！やはり最終的には、自分の身は自分で守らなきゃイケないんですかね。。
じうーこ 2011年1月5日 15:04 こんにちは♪Lさん！何となく分かった様な分からない様な・・・良くこんな文章かけるね！頭良い証拠だわ！おっちゃんちょっと眠くなって来た。。。様はセキュリティは万全にしろと言う事ですね♪	コメントへの返答 2011年1月5日 19:45 じうーこさん、こんばんわ＾＾大学の優秀な研究員さんのお陰ですよ！僕は何度も読返して理解しましたから、頭良くないですよ（≧≦）はい、お互い気をつけましょうね♪
彩葉 2011年1月5日 15:28 数字苦手なので　ヽ(+∇+)ノ・・・キュゥ　状態ですセキュリティ対策をしても、被害に遭う方がいらっしゃる。本当に腹立たしいですヾ(o｀皿´o)ノ＠)) 暮れにセルシオの盗難が増えているという記事を読みましたが、やっぱりハイエースなんですね(；´ω｀)ﾀﾗｰﾘ･･･	コメントへの返答 2011年1月5日 19:49 僕も理解するまでに、頭ショートしそうになりました。。。人の気持ちがどれだけ傷付くのか、分からないんでしょうね（≧≦）ハイエースは海外でも大人気みたいですね。日本車はガソリン車も、ディーゼル車も、20万km以上走っても、ノントラブルですもん！
匠~TAKUMI~ 2011年1月5日 18:17 理系大卒なんですが途中から理解するのを諦めました(汗)	コメントへの返答 2011年1月5日 19:52 お忙しい中、長文すいません（≧≦）理系かじってらっしゃいますし、僕より早く理解できるて思いますよ＾＾僕は時間かかりましたから。。
ドン・コルレオーネ 2011年1月5日 18:31 お邪魔しました（爆）過去に所有していたセルシオ（３０後期）も、イモビを解読され同モデルの盗難が多発しているそうです。窃盗団も”イモビカッター”を使い瞬時に持ち去る手口・・・まぁ時間の問題だと思ってましたが(>_<) と、こんなもんで如何でしょうか"^_^" 今夜、、、夢●しそうです（謎爆）	コメントへの返答 2011年1月5日 19:55 ウケましたwww 1度解読されてしまうと、簡単に持ち去られてしまいますから、やはり物理的セキリュティが必要になってきますよね（≧≦）楽しい夜になりそうですね(￣―＋￣)
せきとり 2011年1月5日 19:35 食いもんの話ちゃうのん？ (´0`)ふぁ~	コメントへの返答 2011年1月5日 19:56 どう連想したら食いもんの話になるんすかwww
ＨＩＳＡ 2011年1月7日 6:23 途中で頭から煙がモクモクでてきましたｗｗこういう難しい話はＰＣの画面より紙の方が見やすいですね！	コメントへの返答 2011年1月7日 9:08 分かりにくい書き方しちゃったね（≧≦）確かにwww 項目別に頁分けたら見やすかったんだけど、ひとつにまとめちゃった(^_^;)
フェローズ 2011年1月7日 9:51 やっと解けたよ（汗）てかほんとこの素因数分解ってほんと不思議よね。暗号鍵と複合鍵、文章と計算式ずっと睨めっこしてたから頭痛いわ！	コメントへの返答 2011年1月7日 10:11 おめでとう♪ 俺もすぐに解けなかったよ(^_^;) 4桁になると、いきなり素因数分解は難しくなるよね。今日は数字見ないで仕事しなさいwww て仕事柄無理か。。。

	アウディ Q2 21年モデルにMCしたらTTから乗り換えで購入したいと思います。 A1からの乗換で当初は ...
	アウディ R8 （クーペ）やはり普段乗る分にも快適に速いAudi技術の結晶年式 : 2021年式グレード : ...
	アウディ A1 スポーツバック街乗り専用車🚘✨✨✨ 2023年7月にQ2君と入替です🚘🚘
	アウディ R8 （クーペ）街乗からサーキットまで優雅に熟すAudi技術の結晶 2日間お借りして、スーパーカーとし ...

容疑者Aの本能 ≡ 数学者Bの挑戦（mod盗難車Xのメッセージ）　　　（PC）

タグ

今、あなたにおすすめ