先々週の水曜日から喉が痛くて熱も出たので1週間会社を休んだのですが、まだ喉が痛くて咳が止まらず困っております。
火曜日は耳鼻科に行って診てもらったのですが、お医者さんからは
「お前はすでに治っている!。」
と言われて帰ってきました。
確かに、全く声の出ない状態から普通に声は出るようになったのですが、いまだに咳が止まりません。
早く治って欲しいものです。
さて、そんな今日このごろではありますが、今日は鈴鹿サーキットの1~2コーナの走行ラインを考えたいと思います。
実測結果やシミュレーション結果ををたくさん見てわかってきのですが、仮に走行ラインが理論上最適でなくても、その走行ライン上をタイヤの摩擦円の縁で走れれば、十分速いタイムで走れるし、逆に走行ラインが理論上最適だったとしても、実際にそのライン上を摩擦円の縁で走ることができなければ、いまいちなタイムでしか走れません。
したがって、目指すべきところは理論上最適な走行ラインをタイヤの摩擦円の縁で走ることなのですが、もしタイヤの摩擦円の縁で走ることができないとするならば、タイヤの摩擦円の縁で走ることができるような走行ラインに少しずつ変えていくことが次善の策ということになろうかと思います。
ということを念頭において鈴鹿サーキットの1~2コーナについて考えてみましょう。
鈴鹿サーキット1~2コーナは、1コーナをコーナとして考えるべきなのか、日光サーキットの1~2コーナと同じように2コーナの入り口が曲がっているだけと考えるべきなのか、コース図を見ただけではわかりずらいです。
そこで、日光のときと同様に作図法で各コーナの最低速度を求めます。
まずは、コースの内外に接する最大の円を描きます。

次に推奨半径を計算で求め、作図します。

計算結果と図からそれぞれの最低速度と最低速度間の距離を求めます。
今回は最大横Gを1.35G、最大減速G:0.95GのFD2シビックを例題として考えることにします。
1コーナ:162km/h (700m地点)
2コーナ:101Km/h (850m地点)
コーナ間距離:150m
ここで、1コーナから2コーナの最低速度である101km/hへ減速するために必要な減速Gが0.95Gよりも十分大きければ、日光と同様に1コーナはコーナとして考える必要がありません。
計算は省略しますが、150mで1コーナと2コーナの速度差61km/hを減速するために必要な減速Gは0.42Gです。
曲がりながら減速する必要があるので、0.95Gは無理としても0.6Gくらいで減速できるような気がします。
実際に発生できる減速Gよりも必要な減速Gの方が小さいので、この計算からは別々のコーナとして考えた方がいいように思います。
しかし、これではよくわからないので、シミュレーションをしてみました。
赤:シミュレーション
青:FD2実測
水色:旋回半径

ラップタイム:143.32秒
このシミュレーションは半径推奨の図でR153の円とR59の円を黒太線でなめらかにつないだ走行ラインで計算しています。
実際にシミュレーションに使った走行ライン
赤:シミュレーション
青:FD2実測

作図法で考えたとおりに、1コーナと2コーナは別々のコーナとして曲がっているような走り方が最適という結果になりました。
この走行ラインでも走れなくはなさそうなのですが、最小旋回半径で走行する距離は極力短くした方がタイム的に速く、半径一定の区間が長いと走りづらいので、2コーナの最小旋回半径地点まで徐々に半径を小さくするような走行ラインに変えた方が良いと思われます。
しかし、1コーナとのつながりを考慮すると、今以上に外側から2コーナに進入することができません。
そこで、1コーナの半径をさらに小さくします。
どのくらい小さくすべきなのかという目安がないので、今回は、1コーナの最小旋回半径の円が2コーナの最小旋回半径の円と重なるような半径に設定しました。
作図するとこんな感じになります。

さらに走行ラインを描きます。

1コーナの最小旋回半径は131mまで小さくなりました。
速度も150km/hまで低下します。
この走行ラインでシミュレーションをした結果がこちらです。

ラップタイム:143.34秒
速度変化は実測結果とかなり近くなりました。
ただ、2コーナの最低速度がシミュレーションの方が遅いので、さらに2コーナの半径を大きくしました。
2コーナ半径62m

走行ライン

ラップタイム:143.27
速度変化も走行ラインも実測と同じようになりました。
今回の検討では実測と合わせ込むことが目的ではなかったのですが、結果的には実測と同じような走行ラインにしたときが最も速く走れそうだということがわかりました。
しかし、どの走り方をしても0.1秒も差がないので、実際はタイヤの摩擦円の縁を使って確実に走れる走り方をするのがよいと思います。
最後におまけで、1コーナと2コーナをなめらかな曲線で繋いだ場合のシミュレーション結果です。
他の走り方よりも0.2秒近く速いのですが、この走行ラインは760m付近で若干コースをはみ出すところがあるので、残念ながら実際には走れないと思います。

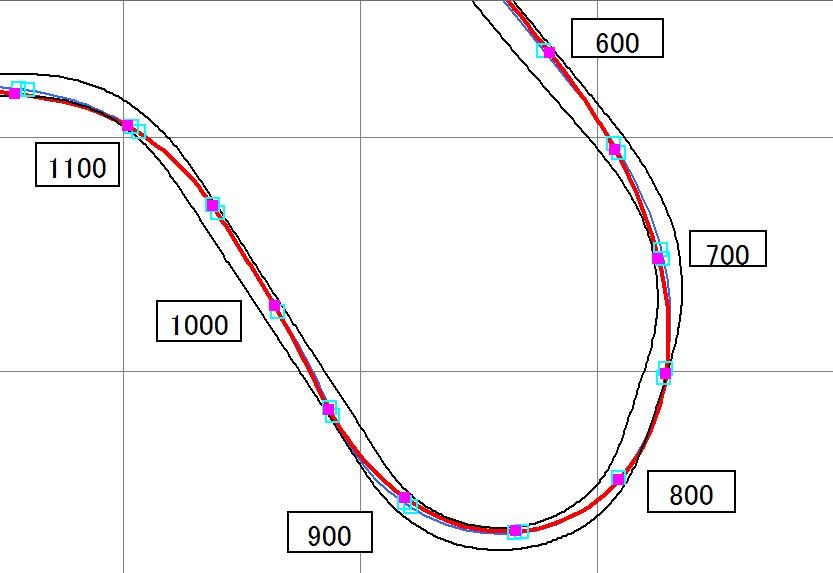
ラップタイム:143.10秒
ということで、走り方(走行ライン)に迷ったら、作図法であたりをつけて、シミュレーションをしてみると、具体的な走行ラインの目標ができるので大変オススメです。
補足
コーナ間で必用な減速Gを求める式です。
減速G:a(m/sec2)
最低速度:V0(m/s)
コーナ間速度差:⊿V(m/s)
減速区間:L(m)
a=(⊿V^2+2×⊿V×V0))/(2×L)
今回の場合
最低速度:V0=28.06(m/s)(101km/h)
コーナ間速度差:⊿V=16.94(m/s)(61km/h)
減速区間:L=150(m)
必用な減速G
a=(16.94^2+2×16.94×28.06))/(2×150)
=4.13(m/s)
=0.42G














