タツゥのブログ一覧

写真は4月5日に行ってきたF1 TOKYO FAN FESTIVAL 2025に展示されていたレッドブルRB16Bです。

僕は予選の日のみ行ってきました。
この日は角田選手初のレッドブルでの予選ということで、パブリックビューイングでの観戦は大いに盛り上がりました。

では、前回の続きです。

今のところの結論は
日本式：最低速度までブレーキで減速する走り方
欧州式：コーナの途中から最低速度までをエンジンブレーキのみで減速する走り方
ということになっていますが、オートスポーツに書かれていた欧州式では①ブレーキは直線で終わらせる、②コーナは一定速度という二つの特徴があります。

しかし、僕の考える欧州式ではコーナ中もブレーキで減速していて、途中からエンジブレーキで減速することになっているので、①②どちらにも合っていません。

ところで以前、僕がこの問題で悩んでいるときに、僕の知り合いで一番速い人に、どういうことなのか聞いてみたことがあります。

すると以下のような回答をもらいました。
「ブレーキを急に弱くする間に大きくハンドルを切るので、そこから先がその人にとってはコーナと考えている可能性がある」

つまり、実際にはクルマは曲がっていて、コーナでも減速しているが、「ブレーキを強く踏んでいて舵角が小さい間はコーナではなく、直線である。」という考え方です。

そんなことある？？って最初は思いましたが、あらゆる可能性を排除しないのが最近の世の中の流行なので、この考え方を取り入れると、①の「ブレーキは直線で終わらせる」については「舵角が小さく、ブレーキを強く踏んでいる区間を直線とする」と置き換えることができます。

同様に②の「コーナは一定速度」についても、これは「ブレーキを非常に弱く踏んでいる区間はほぼ一定速度である」と考えれば説明ができます。

実際にコーナ(走行ラインが曲線)かどうか、一定速度かどうかではなくて、そのドライバーがどう考えているかで判断します。

これを速度変化グラフで表す下図のようになります。


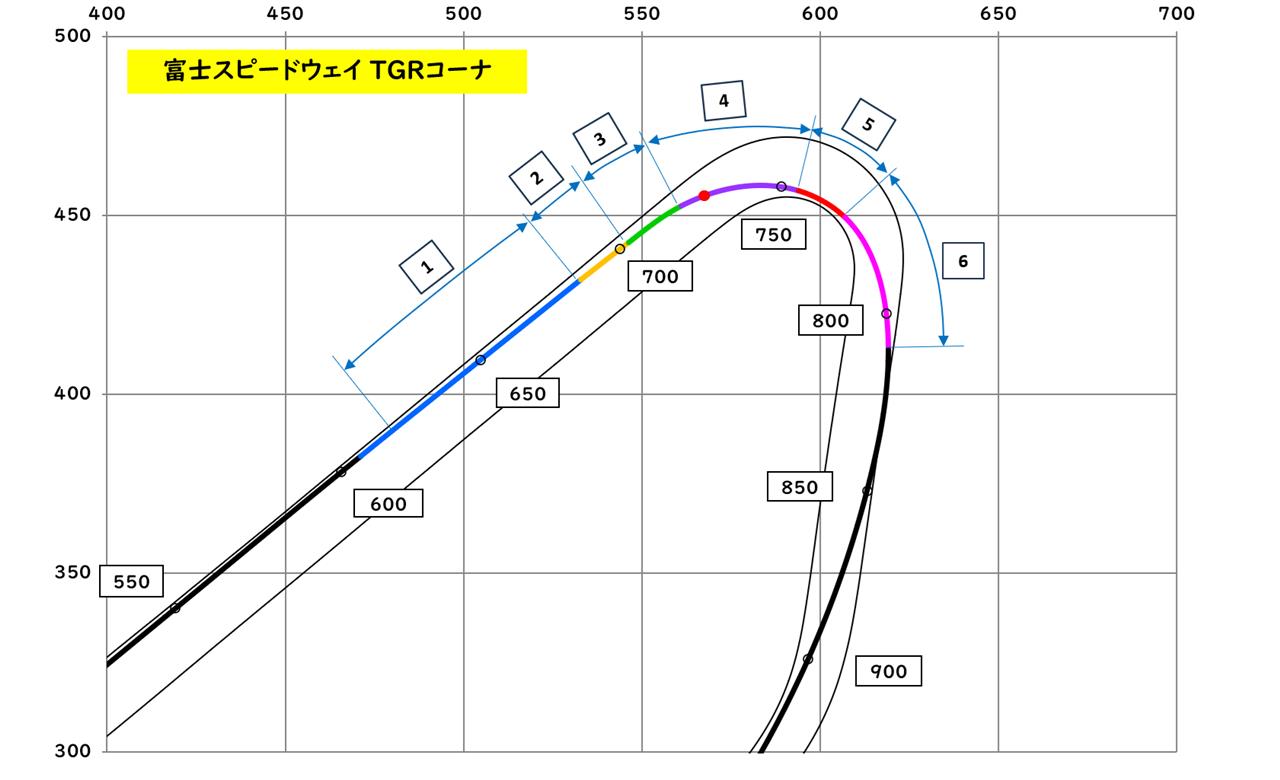
走行ラインで表すとこのようになります。
桃色線がドライバーの考えるコーナです。


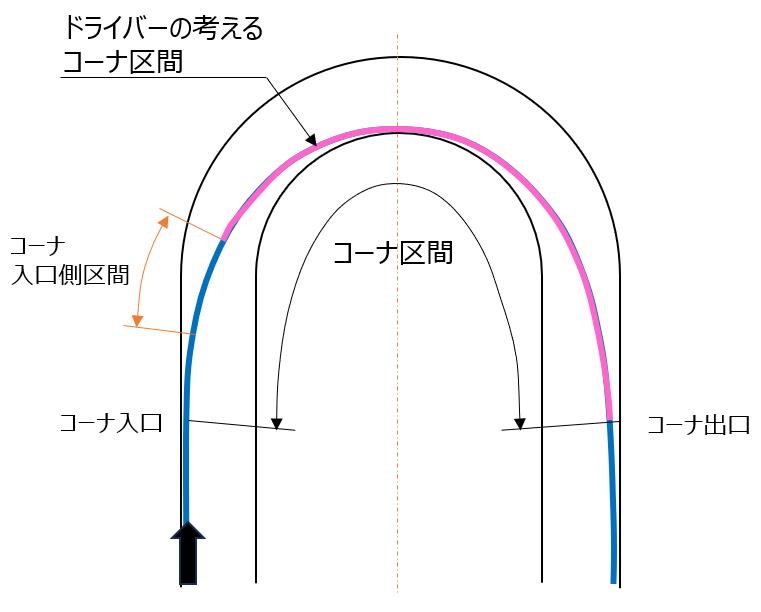
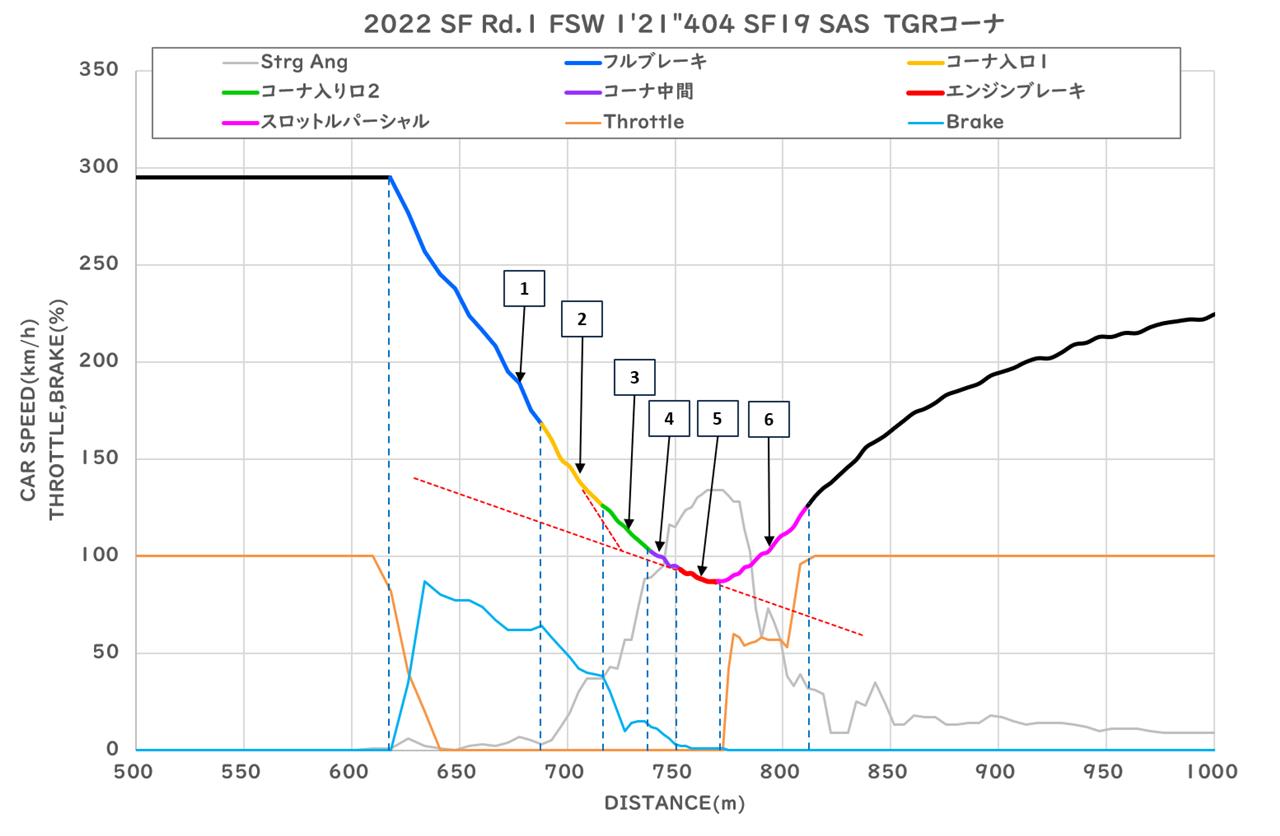
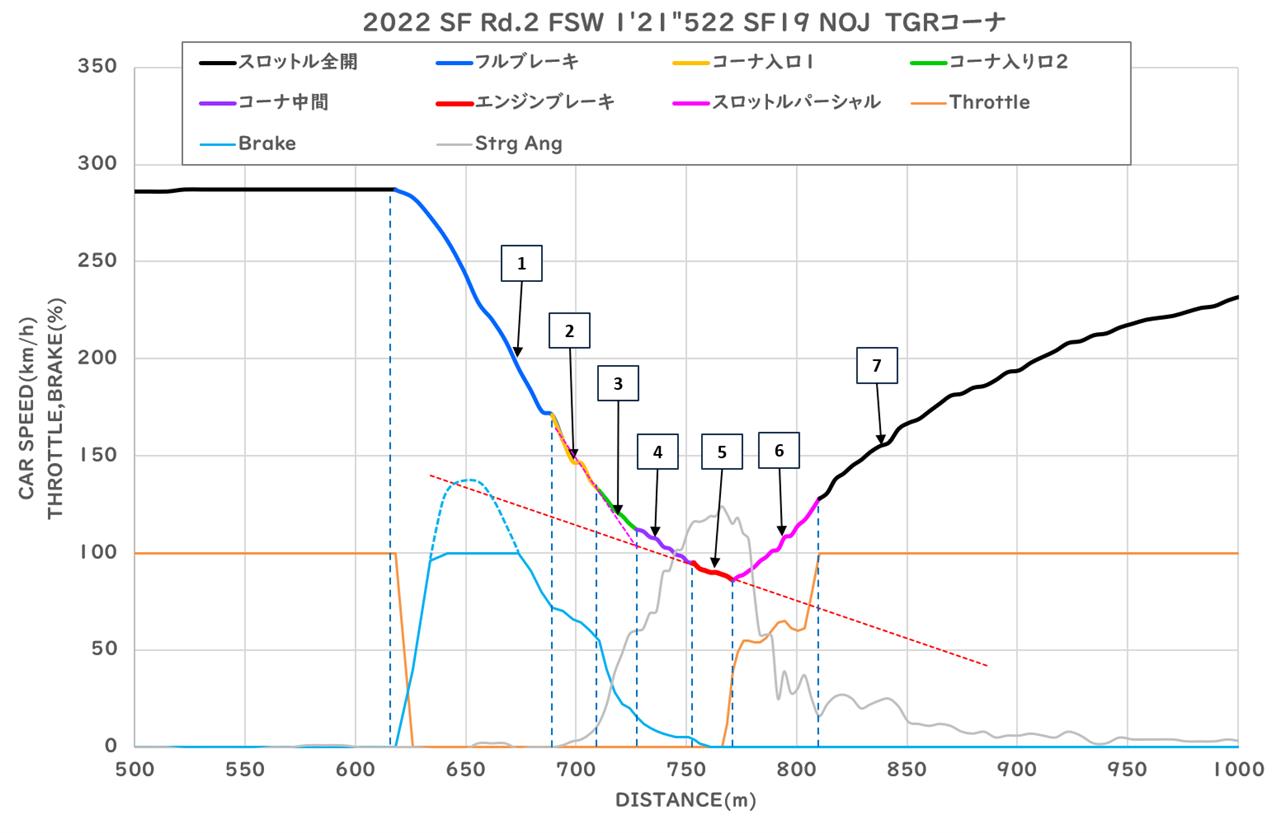
このような速度変化をしていれば、欧州式コーナリングだということにして、スーパーフォーミュラ野尻選手の富士スピードウェイ TGRコーナの走行データを見てみることにします。


※走行ラインは僕の推測で多少ズレている可能性があります。


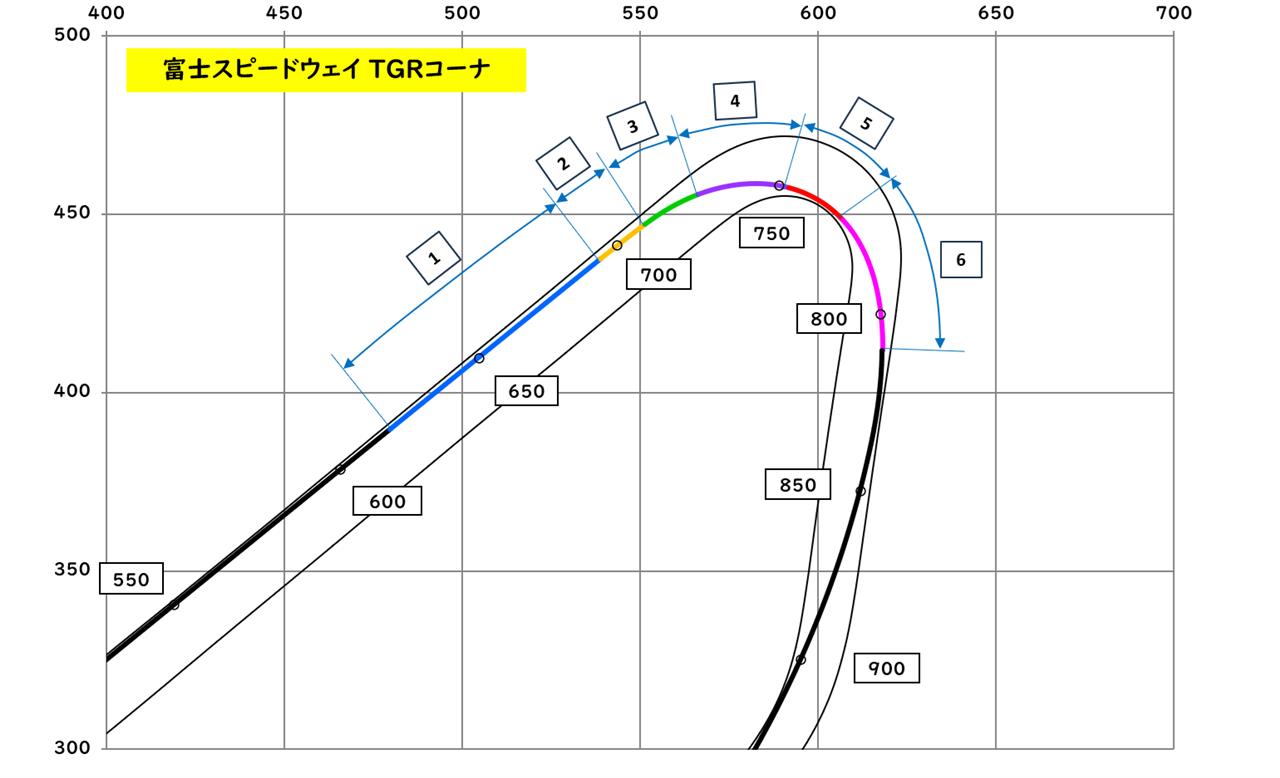
野尻選手のTGRコーナの場合は②の区間の舵角が小さく、③の区間で短時間でブレーキを弱くして舵角が大きくなっているので、③区間の途中までが直線で、③区間の途中と④⑤区間をコーナということにすれば、ブレーキは直線で終わらせて、コーナ中は一定速度（実際はブレーキが弱いだけ）と言えるので、欧州式コーナリングに分類されると考えられます。

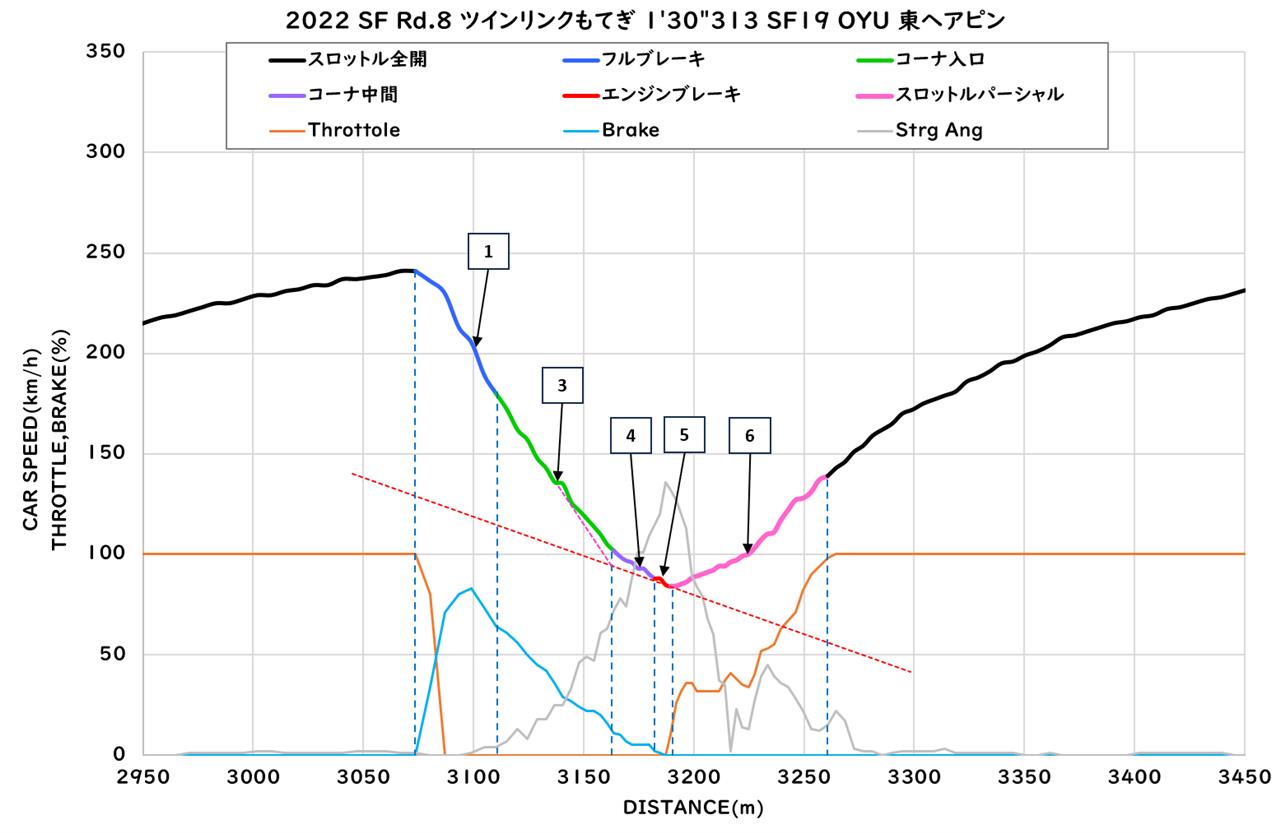
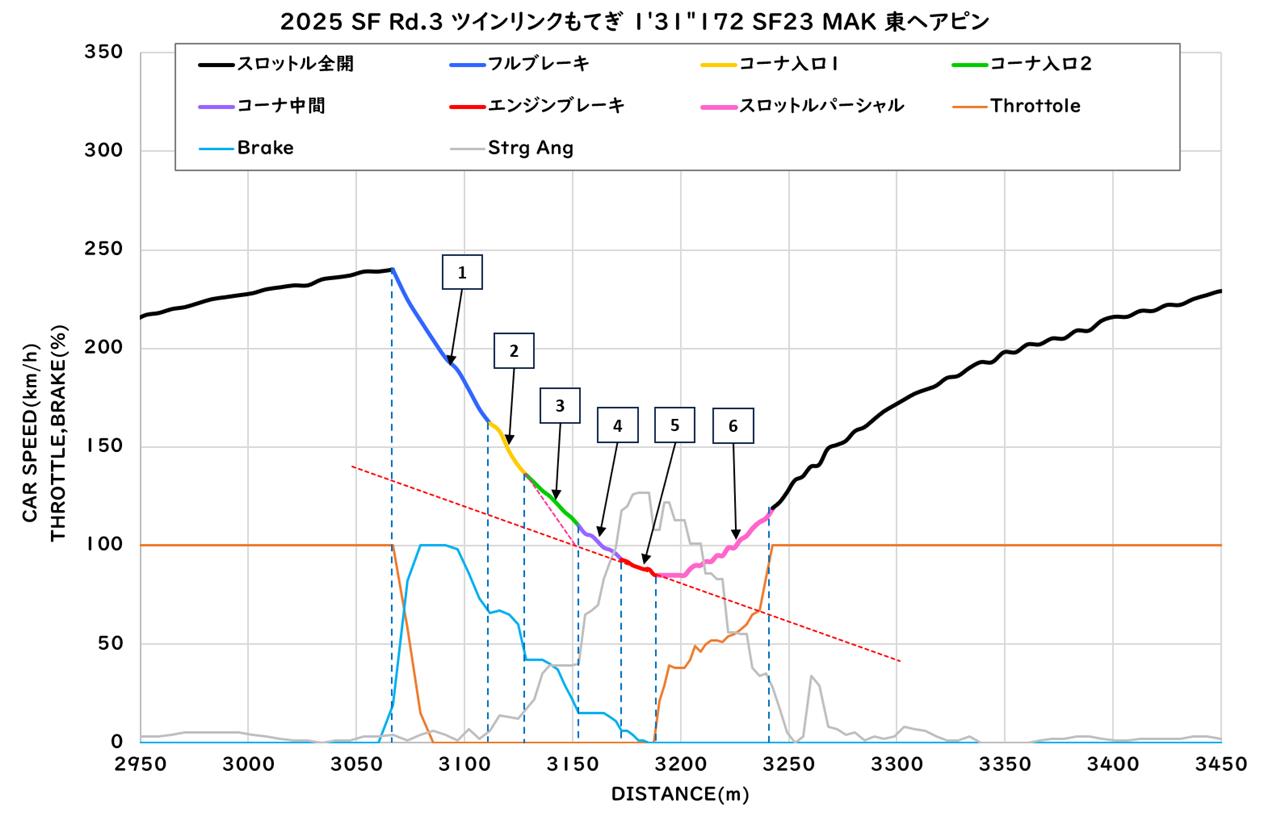
次に、エンジブレーキ区間が短い大湯選手のもてぎ東ヘアピンの走行データを見てみます。



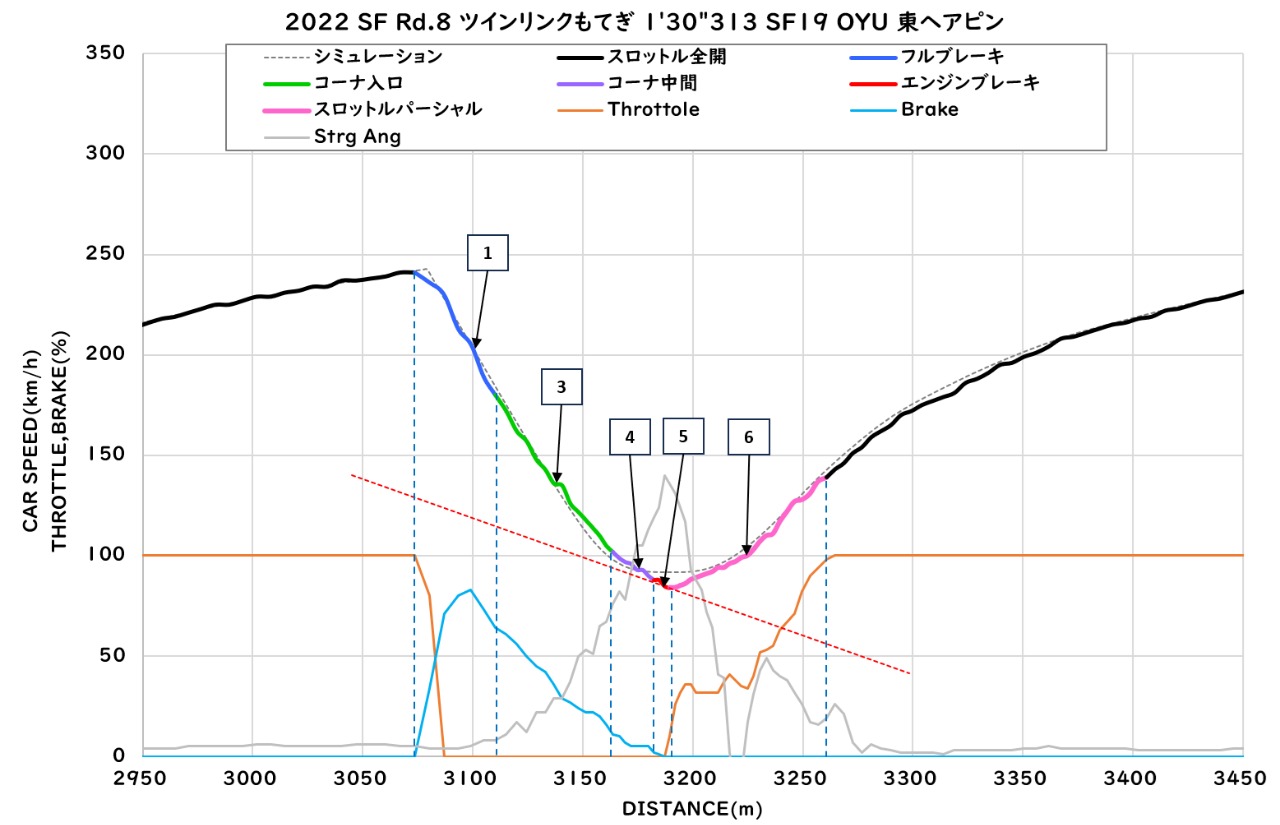
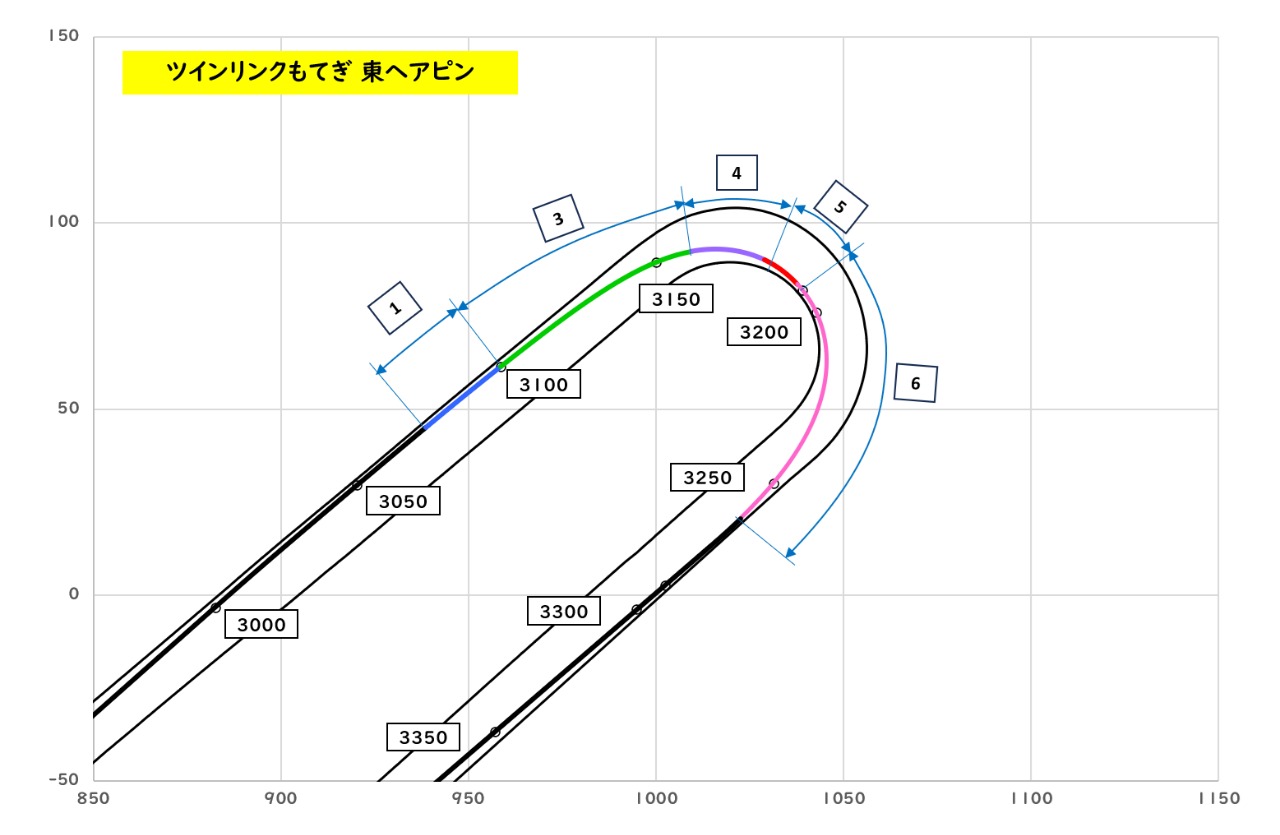
大湯選手の走行データでは、エンジブレーキ区間が短いという特徴があるのですが、もうひとつ特徴があります。
それは、速度変化の折れ点(③と④の変化位置)がコーナ中央寄りにあるということです。

今まではエンジンブレーキ区間の長さの違いが欧州式と日本式の違いだと考えていましたが、エンジンブレーキ区間の長さの違いは、速度変化の折れ点の位置の違いによる結果であって、速度変化の折れ点の位置の方が大事なのではないかと気が付きました。

速度変化の折れ点がコーナ入口側に寄っていると、残りのコーナをブレーキが弱い状態で減速することになり、その分エンジンブレーキ区間も長くなるので、本質は速度変化の折れ点位置の方ではないかと思います。


またまた結論が変わったので、これまでの欧州式と日本式の違いに関する結論に出てきたキーワードを表にまとめてみました。


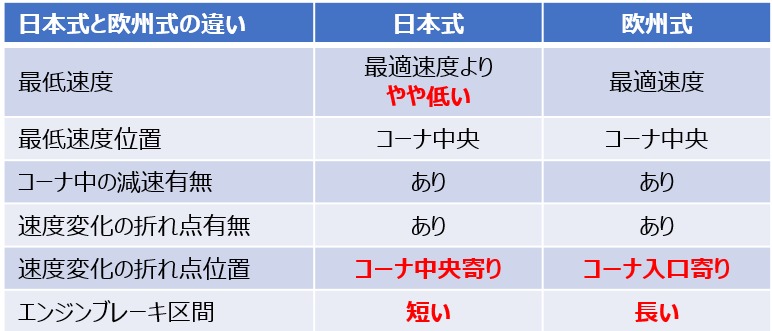
以前、日本式も欧州式も最低速度に差はないと書きましたが、コーナ中の最適速度からの差を全体的に小さくしようとすると、日本式では最適速度よりも最低速度を少し低くしないとコーナ中央寄りに速度変化の折れ点を設定できないので、恐らく日本式コーナリングでは最低速度が最適速度よりも少し低くなっていると思います。



さらに欧州式と日本式の速度変化を模式図で表すと下図のようになります。

欧州式の速度変化(桃色点線が日本式)


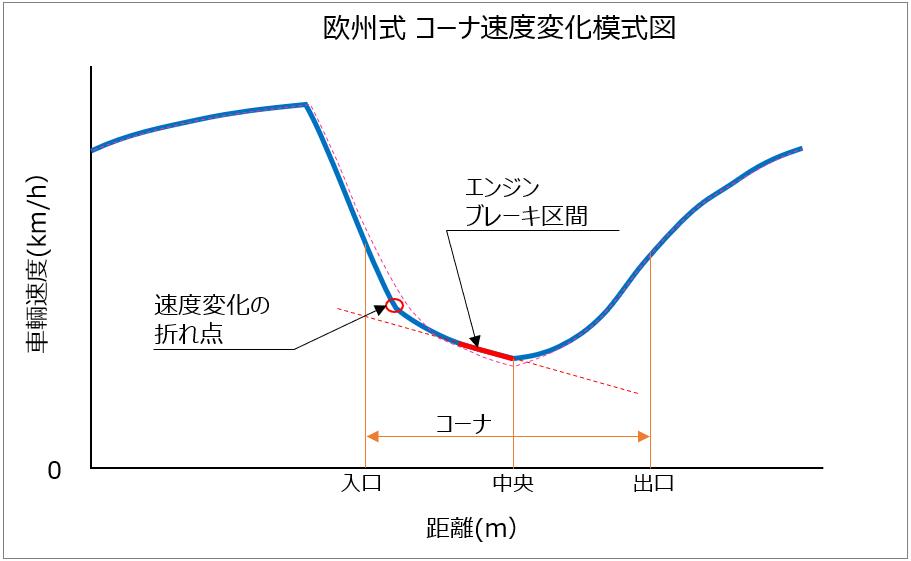
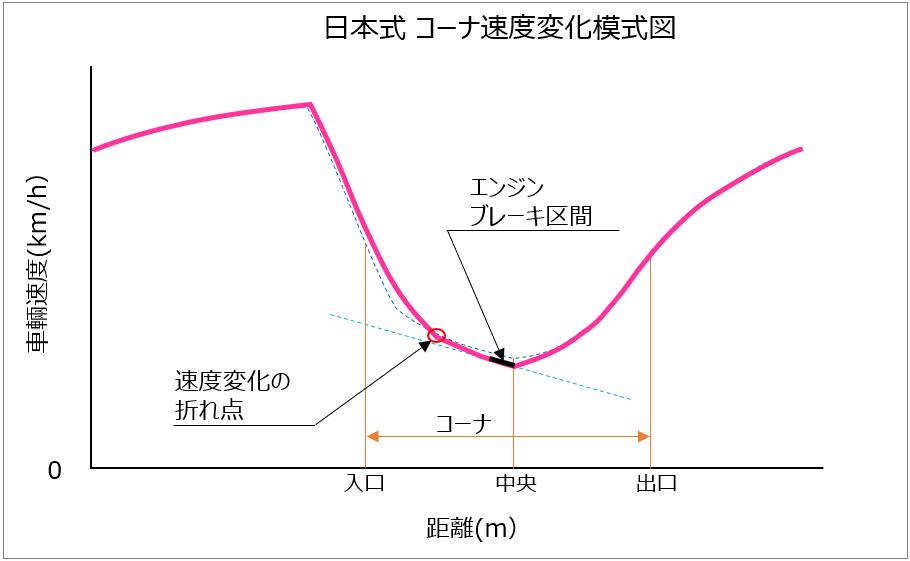
日本式の速度変化(青色点線が欧州式)


ブレーキ強さ変化


速度変化は、ぱっと見はどちらも同じで、どちらもコーナ中に減速してるし、コーナ中の速度変化に折れ点もあるし、最低速度の差も小さいので、片方だけ見てもすぐにはどちらがどちらか判断しにくいのが実態です。

しかし、コーナ中の速度変化の折れ点がコーナの入り口側に寄っているか、コーナ中央側に寄っているかを確認すると、どちらかを判断しやすくなります。

では、例題として欧州ドライバーのフェルスタッペン選手のハンガロリンク１コーナの走行データを見てみましょう。




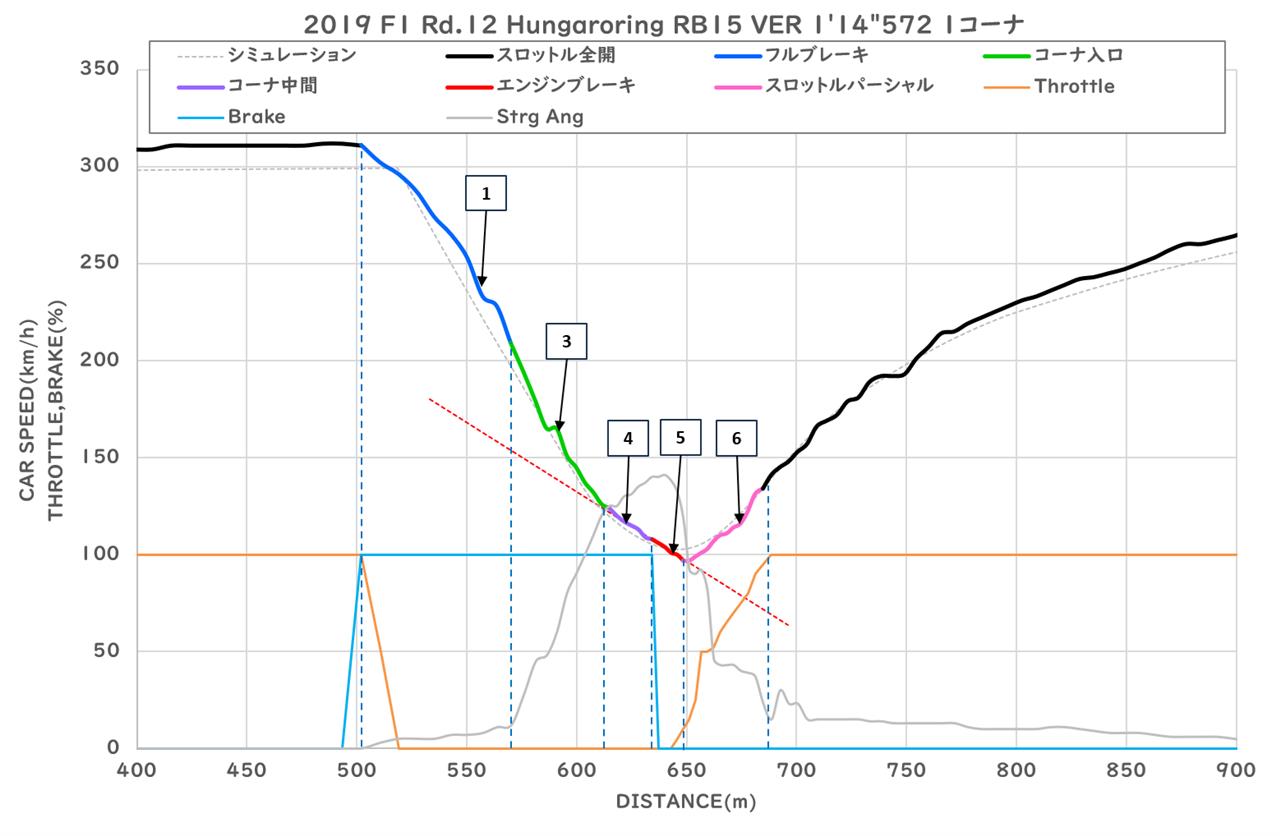
見てわかるとおり、タッペン選手の走行データでは、速度変化の折れ点(③と④の変化位置)がコーナ中央寄りになっています。

したがって欧州人のタッペン選手は日本式コーナリングで走っているということになります。

ここで、さらによく見てみるとタッペン選手の場合速度変化の折れ点以降の④と⑤区間の速度変化がほぼエンジンブレーキの速度変化になっていることがわかります。

エンジブレーキ区間の長さだけで判断すると、このタッペン選手の走行データは欧州式になるのですが、速度変化の折れ点の位置で判断すると日本式となり、速度変化や舵角変化を見る限り野尻選手よりも大湯選手に近い走り方になっているので、エンジンブレーキ区間の長さではなく、速度変化の折れ点位置で判断する方が正しいように思いました。

ではなぜ大湯選手はエンジンブレーキ区間が短いのか？と疑問に思う人もいると思うので、大湯選手の走行データにRB15のエンジブレーキ相当速度変化を重ねてみます。


こうやって見ると、大湯選手は④区間をRB15のエンジンブレーキ相当の減速Gで減速しているということがわかります。

クルマもコーナも異なるので、実際のところはよくわらないのですが、恐らくどちらも求められる最適な速度変化は同じで、速度変化の折れ点以降の減速Gもほぼ同じ減速Gで減速したいけどF1の場合はエンジブレーキが強いので④区間がほぼエンジブレーキ相当の減速になり、スーパーフォーミュラの場合はエンジブレーキが弱いので、④の区間もブレーキで減速するという走り方になっているだけで、目指している走り方はほぼ同じであるというのが僕の推測です。

では最後にまとめです。
基本的には前述の一覧表や速度変化そのものが日本式と欧州式コーナリングの違いですが、要点を短くまとめると以下になります。
日本式：コーナ中の速度変化折れ点がコーナ中央寄りにある走り方
欧州式：コーナ中の速度変化折れ点がコーナ入口側にある走り方

という結論になりましたが、本当は日本式と欧州式の二つに分類することの意味はあまりないと思ってます。

本来の目的は「コーナ中の最適な速度変化に極力近づけること」なのであって、日本式とか欧州式というのはその方法論のひとつに過ぎないと思うのです。

どちらの方法でも結果的にコーナ中の最適な速度変化に近づけていないのであれば遅いし、近づいていれば速いので実際のクルマやタイヤの特性に合った方法を選ぶべきだと思います。

ということで、やっぱり「コーナ中の最適な速度変化とはなんぞや？」ということが一番大事だということを再認識したので、再び走行ラインの最適化について考えたいと思います。

2013年2月のオートスポーツ1349号の記事から始まったこのコーナーも昨年ようやく自分の納得できる結論を導くことができました。

その後すぐにコーナ走行ラインの最適化に関する新知識を得たことで、まとめを放置しておりましたが、走行ライン最適化に戻る前に欧州式コーナリングのまとめをすることにします。

オートスポーツの記事を読んだ当時は、オートスポーツに記載されているような欧州式でサーキットを走るプロドライバーは僕の知る限りどこにもいないため、「オートスポーツはいったい何が言いたいんだろう？？？」と疑問だらけでイラっとしてましたが今にして思えば、このオートスポーツの記事をきっかけとしてサーキット走行理論の理解が大きく進んだのでオートスポーツに感謝です。

まず今回は僕が過去に書いた内容を振り返り、次回まとめをしたいと思います。

【2013年6月】（ドライビングスタイル）

ここでは最初にオートスポーツ1349号に記載されていたことを以下のようにまとめました。

日本式・・・加減速を重視し、ブレーキはクリッピングまで残す走り方
欧州式・・・コーナリング速度を重視し、減速は直線で終わらせて、コーナは一定速度で走る走り方

この内容に対する僕の考え
１、日本も欧州も大きな違いはなく、そもそもサーキット走行にはいわゆる日本式しかない
２、比較的コーナリング速度重視なのが欧州式で、比較的加減速重視なのが日本式

このときは本当にオートスポーツが何が言いたかったのかさっぱりわからなかったので、日本式と欧州式という違いがあるとするならば、その差は非常に小さいのではないか？という考えを書きました。

ちなみにグランツーリスモのHPでは欧州式という言葉は出てきませんが、コーナの絵と加減速についてオートスポーツ1349号と同様のことが記載してあります。
→コーナリングの考え方

【2014年6月28日】ドライビングスタイル2
【2014年6月30日】ドライビングスタイル２の続き

このときは最適な走り方に違いはないが、最適な走り方への合わせ込み方法に違いがあるのではないか？と考えて、日本式と欧州式の違いを以下のように推定しました。

　日本式・・・最適な走り方に直接合わせ込もうとし、加減速を重視する
　欧州式・・・最適な走り方に速度が高い側から合わせ込もうとし、コーナリング速度を重視する

さらにコーナ最小半径違いでの区間タイムをサーキットシミュレーションで計算し、以下の結果を得ました。

１、最適な最小旋回半径からの差が大きくなるほどラップタイムは遅くなる。
２、最適な最小旋回半径よりも小さい半径を当初目標とすると、減速の途中で修正できない。
３、最適な最小旋回半径よりも大きい半径を当初目標とすると、ラップタイムの落ち幅が小さく、減速途中でも最適な走行ラインに修正できる。

【2014年7月12日】ドライビングスタイル２の続きの続き

ここでは少し考え方を変えて、日本式と欧州式の違いは、コーナ中の最低速度位置の違いであるという説に基づいた計算をしました。

このときの計算結果では、コーナ中の最低速度位置を奥にした方速いという結果とともに、最低速度位置を奥にするためにはブレーキを残さないような走り方にする必要があるということがわかり、これが欧州式を指していると推定しました。

【2019年7月21日】ドライビングスタイル3

このときはジェンソン・バトン選手が市販車のシビックタイプRをハンガロリンクを走行したときのデータから以下の推測をしました。

欧州式コーナリングとはコーナ中の減速Gが急に低下するような走らせ方のことを指していて、実際にはブレーキを踏んでいるもののコーナ中に急激にブレーキを緩めるためブレーキを踏んでいないと思い込んでいる可能性がある。

【2021年12月15日】S2000エンジンブレーキ減速G

ブレーキを踏んでいるかどうかを速度変化から読み取ることができるように、S2000のエンジンブレーキの減速時速度変化を確認しました。

【2024年3月20日】最低速度位置とラップタイムの関係(HGR CIVIC TYPE-R再計算)
【2024年3月28日】最低速度位置の向きとラップタイムの関係(SF19 FSW再計算)

ドライビングスタイル3で欧州式コーナリングについて一応の結論を得たものの、「コーナ中の最低速度位置を奥にした方速い」という理論の根拠が乏しかったため、再計算をした結果、以下のことがわかりました。

１、最低速度位置はコーナ中央の方が速い
　　また、以前の計算でコーナの奥側とした地点は実際はコーナ中央付近だった。
２、減速Gが急に低下するような走り方をしなくても最低速度位置を奥(実際はコーナ中央)にすることは可能。

ここでは減速Gが急に低下するような（＝減速時の速度変化に折れ点があるような)走り方は理論上最適な走り方ではないということがわかりました。

【2024年4月3日】レーシングドライバーの減速区間走り方分析(シビックタイプR)

理論上の最適な走り方ではないにも関わらず、多くのレーシングドライバーが減速Gが急に低下するような(減速時の速度変化に折れ点がある)走らせ方をしている理由を最速ラインとの速度、半径変化の比較を行い以下の推測をしました。

①最低速度直前の減速Gはエンジンブレーキの減速Gよりも低く走れない。
　　　　　　　　↓
②最低速度直前の半径が最速ラインよりも大きくなる。
　　　　　　　　↓
③最低速度直前の向き変化が少なくなるため、コーナ入り口の半径を小さくする必要がある。
　　　　　　　　↓
④フルブレーキ区間の後に急に半径を小さくする必要があるので、速度変化に折れ点ができる。

つまり、エンジンブレーキより低い減速Gで走行することが困難なために、レーシングドライバーは減速時に折れ点があるような走り方をすると推定しました。

【2024年4月11日】レーシングドライバーの減速区間走り方分析(SF19 TRM)

そしてついに”欧州式コーナリングとは何を指しているのか”がわかりました。

日本式：最低速度までブレーキで減速する走り方
欧州式：コーナの途中から最低速度までをエンジンブレーキのみで減速する走り方

なぜこんな簡単なことが10年以上わからなかったのか考えてみました。

その理由は
オートスポーツには欧州式ではコーナ入口か中央までを一定速で走ると記載されており、かつF1やスーパーフォーミュラのエンジンブレーキのみの減速Gが予想以上に大きく、エンジンブレーキ区間もブレーキを踏んでいると思っていたからです。

しかし、最近時はF1もスーパーフォーミュラもテレメトリーデータが公開されていて、速度変化、アクセル開度、ブレーキのon、offがわかるようになり、どこでブレーキを踏んでいて、どこがエンジンブレーキのみの減速で、どこでアクセルを踏み始めているか が具体的にわかるようになりました。

その結果、エンジンブレーキ区間の長短、減速Gのアクセルコントロール有無などがドライバーによって少し異なるということがわかり、ここの違いのことを日本式とか欧州式とか言っているのだろうと推定できるようになりました。

ということで、次回は実際のデータを比較しながら日本式と欧州式コーナリングの違いを説明したいと思います。

今日、YOUTUBEを見ていたら、とても勉強になる動画があったのでそのご紹介です。

実際の測定例などが紹介されており、ダンパー好き必見です！！

先日のブログで「実測結果から伸び側のサスストロークが最大になるときは横Gが最大のとき」と書いていて、実際の測定結果もそうなっていたのですが、計算上もそうなんだっけ？と思い、計算しました。

結論から言うと、「計算上は、伸び側のサスストロークが最大になるときは横Gが最大のときではない」という結果になりました。

認識が間違っており大変申し訳ありません。

では計算の説明です。

まず、もう一度サスストロークの計算式のおさらいをします。

サスストロークの計算式
　L＝L1× (1 + ay・ky + ax・kx) + L0・・・式1

ay：前後G、ax：左右G、ky：前後G係数、kx：左右G係数、L0：0Gバネ遊び量、L1：1G縮み量(遊び分を除く）、L：サスストローク

式1を見ると前後G係数と左右G係数の大きさによっては必ずしも横Gが最大のときサスストロークが最大になるとは限らないように見えます。

ここで、ayとaxが摩擦円の式に当てはまると考えて、サスストロークLを計算してみます。

ayとaxが下式の関係にあるとき、摩擦円の式に当てはまることになるので、下式からaxに対するayを求めます。

(ax／axmax)^2+(ay／aymax)^2＝1・・・式2
(axmax：最大横G、aymax：最大前後G）

次に、式2で求めたax、ayを式1に代入してサスストロークを算出します。

以上の計算から横加速度に対する前後加速度とサスストロークの値を求めることができます。

この3つの関係をわかりやすく表す方法を考えた結果、axとayを組み合わせて車輛加速度の方向で表すことにしました。

車輛加速度の方向＝Atan(ax／ay）

なんだかよくわからなかったと思いますが、axmax＝1.15、aymax＝0.95で計算したサスストロークをホイールストロークに換算してグラフにするとこうなります。

横軸が加速度方向、縦軸がホイールストロークです。
加速度方向は、0°が前後方向、90°が左右方向です。


グラフを見てわかるように、僕のS2000の場合、計算上は加速度の方向が60～70°のときに後輪のホイールストロークが最大になりました。

ホントかよ！って思ったので改めて実測結果を確認します。

日光サーキット走行時の実測結果にさきほどの計算値を重ねました。
このときは左後輪にしかストロークセンサーがなかったので、左後輪のデータです。
日光サーキットは右回りで、左後輪が伸び側になる左コーナは1コーナしかなく、このデータもほぼ1コーナのものです。


この実測値との比較だけだと合ってるような合ってないような微妙な感じです。
少なくとも加速度方向が60～70°のとき後輪伸び側ストロークが最大になるとは言い切れません。

ちなみにこのときのGサークルはこのようになっていました。


横加速度がマイナスのところが左コーナです。
ホイールストロークを計算したときに使ったGサークル(赤線)に対して、若干低い値ではあるものの、いまいちこれが計算と実測が合わない原因かどうかわかりません。

計算値と実測結果が合わないときはどうするか？

①実測結果を〇造する。
②都合のいい別の実測結果を探してくる。

僕は良い子なので②の都合のいい別の実測結果を探すことにしました。

最初は左後輪のみだったストロークセンサーはその後、左右両方に取り付けたので、両方で測定したTC1000の走行データを確認します。

TC1000も右回りのコースなので、伸び側になる右後輪の測定結果です。


横加速度プラスが右コーナです。


これは具合がいいです。
計算値と実測結果の傾向がおおよそ合っており、加速度方向が60～70°のとき後輪伸び側ストロークが最大になっていました。

しかし、実測結果を見ると、車輛加速度方向80～90°で走行している時間が長く(点が多い)、ホイールストローク変化も大きいので結果的に80～90°のホイールストロークも60～70°と同じくらいのときがあります。

したがって「計算上、最もインリフトしやすい加速度方向は60～70°であるが、実際は加速度方向60～90°の範囲では同程度にインリフトしやすい」ということになりそうです。

本日の所感
計算値と実測値が合って良かった。

突然ですが、今日はインリフトってどういう条件で発生するんだっけ？ということが気になったので計算することにしました。

FF車に乗っている人は後輪のインリフトに悩んでいる人もいるかと思います。
それなりに改造されたレース用車輛でもインリフトしてるので、個人的には放っておけばいい気もしますが放っておけない人もいると思います。

一方、僕の乗っているS2000をはじめ、FR車で後輪のインリフトに悩んでいるという話は聞きません。

そこで、今日は過去の調査、計算結果を用いて(僕の)S2000の後輪がインリフトする条件を考えてみたいと思います。

ここで、まず始めにインリフトした状態の力のつり合いを考えます。

こういう物理現象を考えるときは、とにかく絵を書きます。

図1：タイヤがインリフトする状態

実際はアームを回転させる力とかありますが、今回はインリフトする条件を考えることが目的なので、簡素化してこの図に書いていない力はないことします。

この図1でF1～F5は以下を示します。
F1：バネ反力(kgf)
F2：バネ下重量とダンパーのガス圧による反力(kgf)
F3：タイヤ接地荷重(kgf)
F4：ダンパー最大伸び時のダンパロッド引張力(kgf)
F5：スタビライザー反力(kgf)

次に図1の3つの状態の説明です。

左の絵は平地に静止した状態で置いてあり車重もタイヤも地面が支えています。
地面がないとタイヤが落ちてしまうので、地面は大事です。
このときの力のつり合いはF3＝F1+F2となります。

中央の絵はインリフトした状態です。
このとき、ダンパーは最大に伸びていません。

地面がなくて、ダンパーも最大に伸びていないとタイヤを上に持ち上げてくれる人がいない気もします。

かつて、AE85カローラレビン ライムにはリアスタビライザーがついていませんでしたが、僕のS2000はスポーツカーなのでリアスタビライザーがついていて、インリフトするときは反対側のダンパーは縮んでいるので、スタビライザーがタイヤを上に持ち上げてくれます。
このときの力のつり合いはF5＝F1+F2となります。

右の絵はインリフトした状態で、かつダンパーは最大に伸びています。
中央と同様にスタビライザーは効いているので、スタビライザーもタイヤを上向きに持ち上げていますが、ダンパーロッドもタイヤを上向きに持ち上げています。
このときの力のつり合いはF4＋F5＝F2となります。

仮に僕のS2000がインリフトすることがあったとしたら、それは中央の状態なのか？それとも右の状態なのか？、まずはここを知る必要があります。

整備をするときに片側だけジャッキアップすると、バネを遊ばせるような車高調セットをしていたとしても少しバネが縮んだ状態でタイヤが持ち上がるときがあるので、感覚的には走行時のインリフトは中央の状態だと思っています。

本来は現物の状態を確認した後で計算すべきですが、あいにく修理中で確認できないので、今回は計算だけ行いました。

計算するにあたり、何をどう計算するとわかりやすくて、かつより正しい結果が得られるのだろうと考えた結果、サスペンションのストロークとタイヤの接地荷重を計算するのがわかりやすそうだったので計算しました。

計算は僕のS2000を想定し、以下の条件で計算しました。
1、車輛重量(ドライバー、ガソリン込み)：1340kgf
2、後輪片側バネ下重量：35kgf
3、ダンパーガス圧による反力：20kgf
4、後輪片側バネ上下重量：300kgf　(1340/4－35)
5、リアサスペンション諸元：過去に調べた値→こちら
リアスタビライザーは130用とし、かつメインスプリングはバネレートを16kgf/mmとしました。
6、ダンパー伸び側ストローク最大のときメインスプリング縮み量が0とする。
　(プリロード0でバネの遊びもなし)
7、反対側のタイヤは逆方向に同じだけ動く。

計算結果：ホイールストロークとタイヤ接地荷重


このグラフは車輛が静止、接地した状態のホイールストローク(車体に対するタイヤの上下変位)を0mmとしてダンパー伸び側がマイナス、縮み側をプラスとして、ホイールストロークに対するバネ反力、スタビライザー反力、タイヤ接地荷重をホイール端位置の値で表しています。

タイヤのインリフトという状態は図1のF3(タイヤ接地荷重)が0になったときに発生するので、グラフの赤線を見ることでホイールストロークに対してどこでインリフトが発生するのかがわかります。

今回のS2000の計算結果では、ホイールストロークが-27mmのとき(接地状態から27mm伸びたとき)にタイヤ接地荷重が0kgfになりました。

このときのメインスプリング反力は約70kgfなので、まだダンパーは最大まで伸びていません。

メインスプリングの反力が70kgf、ダンパーガス反力が20kgfもあって、さらにタイヤが地面から浮くためにはバネ下重量35kgfも持ち上げなければならないので、誰かが125kgfの荷重を持ち上げなくてはなりませんが、前述のとおりスタビライザーが持ち上げているため、以前調査したS2000の130型用リアスタビライザーのホイール端バネレートからホイールストロークに対するスタビ反力を計算します。

スタビライザーのホイール端バネレートは約4.6kgf/mm(左右が逆位相時)だったので、ホイールストロークが27mmあると4.6×27＝124(kgf) となりスタビライザーが上に持ち上げているということが確認できました。

ここまでの計算で僕のS2000の後輪がインリフトするときは図1の中央の状態でダンパーは最大まで伸びていない状態ということがわかりました。

次に、インリフト対応として僕の嫌いなヘルパースプリングを追加した状態の計算をしてみます。

ヘルパースプリングの仕様を調べてみると、いろいろ種類があるものの、おおよそバネレートは2kgf/mm、密着ストロークは50mm前後、密着荷重は100kgf前後という仕様であることがわかりました。

そこで今回は以下のヘルパースプリング仕様で計算しました。
バネレート：2kgf/mm
密着ストローク：50mm
密着荷重：100kgf(ホイール端では70kgf)

計算結果：ホイールストロークとタイヤ接地荷重(ヘルパースプリングあり)


今回の計算では偶然にインリフトするホイールストロークでのヘルパースプリング反力とヘルパースプリング密着荷重が同じ値になりました。

つまり、今回のS2000の場合、ヘルパースプリングを入れてもインリフトするまではヘルパースプリングは密着していて、あっても無くても何も変わらないということになります。

インリフトした後もヘルパースプリング反力+ダンパガス反力＋バネ下荷重よりもスタビライザー反力の方が大きいので、タイヤは下に落ちてくることはありません。

ヘルパースプリング付けたらたくさん伸びてインリフトしなくなると思って期待しても実際は何も変わらないってことです。

今回の計算条件ではたまたまインリフト時のヘルパースプリング反力が密着荷重と同じになっただけではあるものの、インリフトするFF車輛を見ていると30～50mmくらい浮いていて、インリフトするまでの伸び側ストロークが10mmや20mm伸びたところで解決するとは思えません。

ヘルパースプリングの文句はこのくらいにして、車輛に働く横Gとインリフトの関係について考えることにします。

はじめに過去に僕のS2000で実測したダンパーストロークをホイールストロークに換算した結果を確認します。

図2：S2000 日光サーキット走行データ


さきほどの計算結果から、後輪がインリフトするホイールストロークは27mmということがわかりましたが、実測結果から走行時の伸び側のホイールストロークは19mm程度しかなく、インリフトに対しては余裕があることがわかります。

次にサスストロークの計算式から横Ｇに対するホイールストロークの計算式を求めます。

サスストロークの計算式
　L＝L1× (1 + ay・ky + ax・kx) + L0　・・・式1

ay：前後G、ax：左右G、ky：前後G係数、kx：左右G係数、L0：0Gバネ遊び量、L1：1G縮み量(遊び分を除く）、L：サスストローク

実測結果から伸び側のサスストロークが最大になるときは横Gが最大で、そのときは前後Gが0となっているため式1のay＝0、かつバネ遊び量L0を0、レバー比をγとして式1をホイールストロークLwに書き直すと

　　Lw＝L1・γ・(1+ax・kx)　・・・式2

式2から静止接地時からの変化量⊿Lwを求めると

　　⊿Lw＝L1・γ・ax・kx　　・・・式3

L1、kxを今回の計算結果に合うようにするとL1＝25.17(mm)、kx＝0.366となるので、これを式3に代入します。
また、式3に凹凸による伸び分＋3mmも計算して結果をグラフ化します。



このグラフを見ると、横G+凹凸分のホイールストロークが後輪がインリフトをするホイールストローク27mmを超えるために必要な横Gが1.82gであることがわかります。

したがって、今日のお題であるS2000の後輪がインリフトする条件は、横Gが1.82gを超えたときということがわかりました。

一方、この計算とは別に車輛重心とトレッドで決まる内側のタイヤ荷重が0になる条件があるわけですが、重心高を0.45ｍ、トレッドを1.5mで計算すると1.66gになるので、実際は1.66gを超えた時点でインリフトに関係なくタイヤ接地荷重は0になるため、僕のS2000の場合はインリフトについては気にしなくていいということも今回わかりました。