タツゥのブログ一覧

先日のブログで「実測結果から伸び側のサスストロークが最大になるときは横Gが最大のとき」と書いていて、実際の測定結果もそうなっていたのですが、計算上もそうなんだっけ？と思い、計算しました。

結論から言うと、「計算上は、伸び側のサスストロークが最大になるときは横Gが最大のときではない」という結果になりました。

認識が間違っており大変申し訳ありません。

では計算の説明です。

まず、もう一度サスストロークの計算式のおさらいをします。

サスストロークの計算式
　L＝L1× (1 + ay・ky + ax・kx) + L0・・・式1

ay：前後G、ax：左右G、ky：前後G係数、kx：左右G係数、L0：0Gバネ遊び量、L1：1G縮み量(遊び分を除く）、L：サスストローク

式1を見ると前後G係数と左右G係数の大きさによっては必ずしも横Gが最大のときサスストロークが最大になるとは限らないように見えます。

ここで、ayとaxが摩擦円の式に当てはまると考えて、サスストロークLを計算してみます。

ayとaxが下式の関係にあるとき、摩擦円の式に当てはまることになるので、下式からaxに対するayを求めます。

(ax／axmax)^2+(ay／aymax)^2＝1・・・式2
(axmax：最大横G、aymax：最大前後G）

次に、式2で求めたax、ayを式1に代入してサスストロークを算出します。

以上の計算から横加速度に対する前後加速度とサスストロークの値を求めることができます。

この3つの関係をわかりやすく表す方法を考えた結果、axとayを組み合わせて車輛加速度の方向で表すことにしました。

車輛加速度の方向＝Atan(ax／ay）

なんだかよくわからなかったと思いますが、axmax＝1.15、aymax＝0.95で計算したサスストロークをホイールストロークに換算してグラフにするとこうなります。

横軸が加速度方向、縦軸がホイールストロークです。
加速度方向は、0°が前後方向、90°が左右方向です。


グラフを見てわかるように、僕のS2000の場合、計算上は加速度の方向が60～70°のときに後輪のホイールストロークが最大になりました。

ホントかよ！って思ったので改めて実測結果を確認します。

日光サーキット走行時の実測結果にさきほどの計算値を重ねました。
このときは左後輪にしかストロークセンサーがなかったので、左後輪のデータです。
日光サーキットは右回りで、左後輪が伸び側になる左コーナは1コーナしかなく、このデータもほぼ1コーナのものです。


この実測値との比較だけだと合ってるような合ってないような微妙な感じです。
少なくとも加速度方向が60～70°のとき後輪伸び側ストロークが最大になるとは言い切れません。

ちなみにこのときのGサークルはこのようになっていました。


横加速度がマイナスのところが左コーナです。
ホイールストロークを計算したときに使ったGサークル(赤線)に対して、若干低い値ではあるものの、いまいちこれが計算と実測が合わない原因かどうかわかりません。

計算値と実測結果が合わないときはどうするか？

①実測結果を〇造する。
②都合のいい別の実測結果を探してくる。

僕は良い子なので②の都合のいい別の実測結果を探すことにしました。

最初は左後輪のみだったストロークセンサーはその後、左右両方に取り付けたので、両方で測定したTC1000の走行データを確認します。

TC1000も右回りのコースなので、伸び側になる右後輪の測定結果です。


横加速度プラスが右コーナです。


これは具合がいいです。
計算値と実測結果の傾向がおおよそ合っており、加速度方向が60～70°のとき後輪伸び側ストロークが最大になっていました。

しかし、実測結果を見ると、車輛加速度方向80～90°で走行している時間が長く(点が多い)、ホイールストローク変化も大きいので結果的に80～90°のホイールストロークも60～70°と同じくらいのときがあります。

したがって「計算上、最もインリフトしやすい加速度方向は60～70°であるが、実際は加速度方向60～90°の範囲では同程度にインリフトしやすい」ということになりそうです。

本日の所感
計算値と実測値が合って良かった。

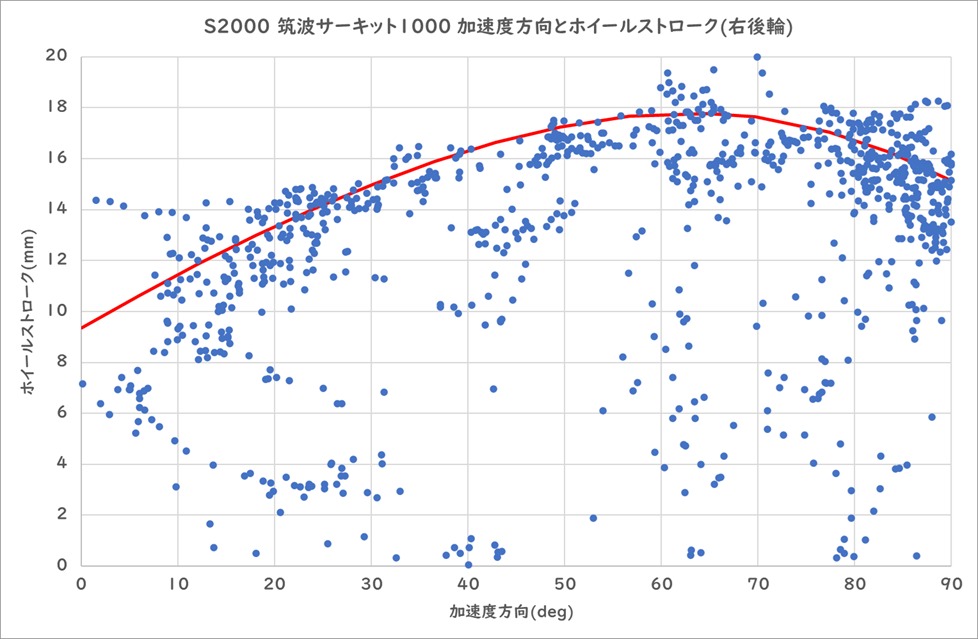
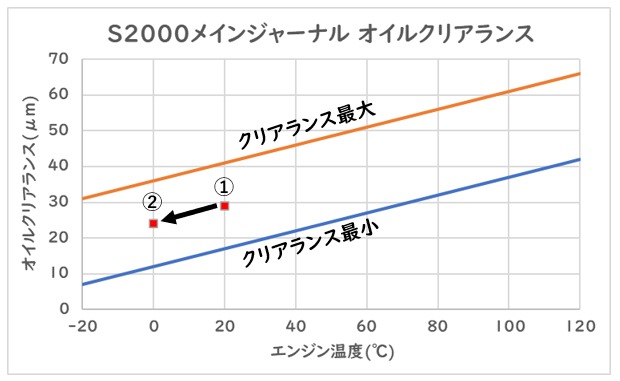
突然ですが、今日はインリフトってどういう条件で発生するんだっけ？ということが気になったので計算することにしました。

FF車に乗っている人は後輪のインリフトに悩んでいる人もいるかと思います。
それなりに改造されたレース用車輛でもインリフトしてるので、個人的には放っておけばいい気もしますが放っておけない人もいると思います。

一方、僕の乗っているS2000をはじめ、FR車で後輪のインリフトに悩んでいるという話は聞きません。

そこで、今日は過去の調査、計算結果を用いて(僕の)S2000の後輪がインリフトする条件を考えてみたいと思います。

ここで、まず始めにインリフトした状態の力のつり合いを考えます。

こういう物理現象を考えるときは、とにかく絵を書きます。

図1：タイヤがインリフトする状態

実際はアームを回転させる力とかありますが、今回はインリフトする条件を考えることが目的なので、簡素化してこの図に書いていない力はないことします。

この図1でF1～F5は以下を示します。
F1：バネ反力(kgf)
F2：バネ下重量とダンパーのガス圧による反力(kgf)
F3：タイヤ接地荷重(kgf)
F4：ダンパー最大伸び時のダンパロッド引張力(kgf)
F5：スタビライザー反力(kgf)

次に図1の3つの状態の説明です。

左の絵は平地に静止した状態で置いてあり車重もタイヤも地面が支えています。
地面がないとタイヤが落ちてしまうので、地面は大事です。
このときの力のつり合いはF3＝F1+F2となります。

中央の絵はインリフトした状態です。
このとき、ダンパーは最大に伸びていません。

地面がなくて、ダンパーも最大に伸びていないとタイヤを上に持ち上げてくれる人がいない気もします。

かつて、AE85カローラレビン ライムにはリアスタビライザーがついていませんでしたが、僕のS2000はスポーツカーなのでリアスタビライザーがついていて、インリフトするときは反対側のダンパーは縮んでいるので、スタビライザーがタイヤを上に持ち上げてくれます。
このときの力のつり合いはF5＝F1+F2となります。

右の絵はインリフトした状態で、かつダンパーは最大に伸びています。
中央と同様にスタビライザーは効いているので、スタビライザーもタイヤを上向きに持ち上げていますが、ダンパーロッドもタイヤを上向きに持ち上げています。
このときの力のつり合いはF4＋F5＝F2となります。

仮に僕のS2000がインリフトすることがあったとしたら、それは中央の状態なのか？それとも右の状態なのか？、まずはここを知る必要があります。

整備をするときに片側だけジャッキアップすると、バネを遊ばせるような車高調セットをしていたとしても少しバネが縮んだ状態でタイヤが持ち上がるときがあるので、感覚的には走行時のインリフトは中央の状態だと思っています。

本来は現物の状態を確認した後で計算すべきですが、あいにく修理中で確認できないので、今回は計算だけ行いました。

計算するにあたり、何をどう計算するとわかりやすくて、かつより正しい結果が得られるのだろうと考えた結果、サスペンションのストロークとタイヤの接地荷重を計算するのがわかりやすそうだったので計算しました。

計算は僕のS2000を想定し、以下の条件で計算しました。
1、車輛重量(ドライバー、ガソリン込み)：1340kgf
2、後輪片側バネ下重量：35kgf
3、ダンパーガス圧による反力：20kgf
4、後輪片側バネ上下重量：300kgf　(1340/4－35)
5、リアサスペンション諸元：過去に調べた値→こちら
リアスタビライザーは130用とし、かつメインスプリングはバネレートを16kgf/mmとしました。
6、ダンパー伸び側ストローク最大のときメインスプリング縮み量が0とする。
　(プリロード0でバネの遊びもなし)
7、反対側のタイヤは逆方向に同じだけ動く。

計算結果：ホイールストロークとタイヤ接地荷重


このグラフは車輛が静止、接地した状態のホイールストローク(車体に対するタイヤの上下変位)を0mmとしてダンパー伸び側がマイナス、縮み側をプラスとして、ホイールストロークに対するバネ反力、スタビライザー反力、タイヤ接地荷重をホイール端位置の値で表しています。

タイヤのインリフトという状態は図1のF3(タイヤ接地荷重)が0になったときに発生するので、グラフの赤線を見ることでホイールストロークに対してどこでインリフトが発生するのかがわかります。

今回のS2000の計算結果では、ホイールストロークが-27mmのとき(接地状態から27mm伸びたとき)にタイヤ接地荷重が0kgfになりました。

このときのメインスプリング反力は約70kgfなので、まだダンパーは最大まで伸びていません。

メインスプリングの反力が70kgf、ダンパーガス反力が20kgfもあって、さらにタイヤが地面から浮くためにはバネ下重量35kgfも持ち上げなければならないので、誰かが125kgfの荷重を持ち上げなくてはなりませんが、前述のとおりスタビライザーが持ち上げているため、以前調査したS2000の130型用リアスタビライザーのホイール端バネレートからホイールストロークに対するスタビ反力を計算します。

スタビライザーのホイール端バネレートは約4.6kgf/mm(左右が逆位相時)だったので、ホイールストロークが27mmあると4.6×27＝124(kgf) となりスタビライザーが上に持ち上げているということが確認できました。

ここまでの計算で僕のS2000の後輪がインリフトするときは図1の中央の状態でダンパーは最大まで伸びていない状態ということがわかりました。

次に、インリフト対応として僕の嫌いなヘルパースプリングを追加した状態の計算をしてみます。

ヘルパースプリングの仕様を調べてみると、いろいろ種類があるものの、おおよそバネレートは2kgf/mm、密着ストロークは50mm前後、密着荷重は100kgf前後という仕様であることがわかりました。

そこで今回は以下のヘルパースプリング仕様で計算しました。
バネレート：2kgf/mm
密着ストローク：50mm
密着荷重：100kgf(ホイール端では70kgf)

計算結果：ホイールストロークとタイヤ接地荷重(ヘルパースプリングあり)


今回の計算では偶然にインリフトするホイールストロークでのヘルパースプリング反力とヘルパースプリング密着荷重が同じ値になりました。

つまり、今回のS2000の場合、ヘルパースプリングを入れてもインリフトするまではヘルパースプリングは密着していて、あっても無くても何も変わらないということになります。

インリフトした後もヘルパースプリング反力+ダンパガス反力＋バネ下荷重よりもスタビライザー反力の方が大きいので、タイヤは下に落ちてくることはありません。

ヘルパースプリング付けたらたくさん伸びてインリフトしなくなると思って期待しても実際は何も変わらないってことです。

今回の計算条件ではたまたまインリフト時のヘルパースプリング反力が密着荷重と同じになっただけではあるものの、インリフトするFF車輛を見ていると30～50mmくらい浮いていて、インリフトするまでの伸び側ストロークが10mmや20mm伸びたところで解決するとは思えません。

ヘルパースプリングの文句はこのくらいにして、車輛に働く横Gとインリフトの関係について考えることにします。

はじめに過去に僕のS2000で実測したダンパーストロークをホイールストロークに換算した結果を確認します。

図2：S2000 日光サーキット走行データ


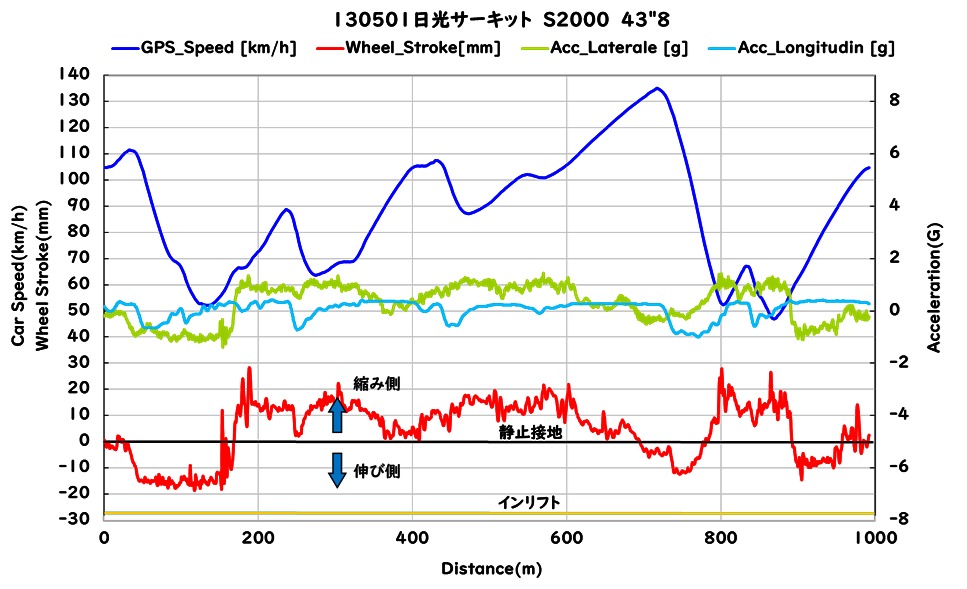
さきほどの計算結果から、後輪がインリフトするホイールストロークは27mmということがわかりましたが、実測結果から走行時の伸び側のホイールストロークは19mm程度しかなく、インリフトに対しては余裕があることがわかります。

次にサスストロークの計算式から横Ｇに対するホイールストロークの計算式を求めます。

サスストロークの計算式
　L＝L1× (1 + ay・ky + ax・kx) + L0　・・・式1

ay：前後G、ax：左右G、ky：前後G係数、kx：左右G係数、L0：0Gバネ遊び量、L1：1G縮み量(遊び分を除く）、L：サスストローク

実測結果から伸び側のサスストロークが最大になるときは横Gが最大で、そのときは前後Gが0となっているため式1のay＝0、かつバネ遊び量L0を0、レバー比をγとして式1をホイールストロークLwに書き直すと

　　Lw＝L1・γ・(1+ax・kx)　・・・式2

式2から静止接地時からの変化量⊿Lwを求めると

　　⊿Lw＝L1・γ・ax・kx　　・・・式3

L1、kxを今回の計算結果に合うようにするとL1＝25.17(mm)、kx＝0.366となるので、これを式3に代入します。
また、式3に凹凸による伸び分＋3mmも計算して結果をグラフ化します。



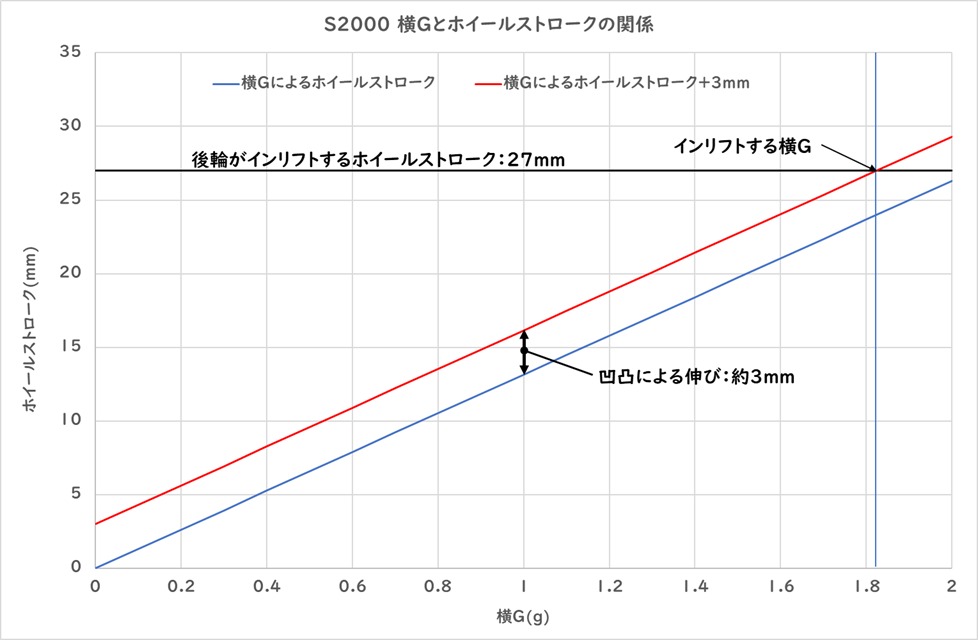
このグラフを見ると、横G+凹凸分のホイールストロークが後輪がインリフトをするホイールストローク27mmを超えるために必要な横Gが1.82gであることがわかります。

したがって、今日のお題であるS2000の後輪がインリフトする条件は、横Gが1.82gを超えたときということがわかりました。

一方、この計算とは別に車輛重心とトレッドで決まる内側のタイヤ荷重が0になる条件があるわけですが、重心高を0.45ｍ、トレッドを1.5mで計算すると1.66gになるので、実際は1.66gを超えた時点でインリフトに関係なくタイヤ接地荷重は0になるため、僕のS2000の場合はインリフトについては気にしなくていいということも今回わかりました。

今の職場に異動してから約３年が経ちました。
通勤では東北新幹線、埼京線、武蔵野線を使っています。

異動後は新型コロナの影響で在宅勤務の日が多かったのですが、昨年GW明けからは出社が多くなり気が付いたことがあります。

埼京線、武蔵野線ではたびたび「体調不良の乗客救護のため遅延が発生しています」という案内があります。

夏は”こんだけ暑かったら体調も悪くなるよなぁ”とか思ってたのですが、実際はあまり季節に関係なく体調が悪い人がいるようで、月に2～3回は遅延が発生してる気がします。

で、ふと思ったのですが、学生～社会人４年目まで電車で通学、通勤をしていた9年間で乗客救護の案内を聞いた記憶がないのです。

学生時代は総武線、京葉線、内房線を使っていて、京葉線は強風、内房線は踏切事故が発生して遅延してましたが、総武線、京葉線含めて乗客救護で遅延があった記憶がありません。

埼京線、武蔵野線の沿線は激務の人が多いのか？とかコロナワクチンのせいなのか？とか、昔は体調不良で倒れてる人がいても無視してたのか？とかいろいろ気になってきました。

なにか理由知ってる人いたら教えてください。

さて、本日の本題です。

今年は暖冬っぽい日が続いてますが、朝はかなり寒くなってきました。
宇都宮は最低気温が-2℃くらいまで気温が下がります。

気温が下がるとS2000のエンジンスターターの回りが悪くなるという問題が発生します。

特に電車通勤するようになってからはほとんどS2000に乗らないのでバッテリーも上がり気味で、先日はエンジンかかる前にバッテリーが上がってしまいました。

で、またふと思ったのです。
スターターの回りが悪い原因はなんだろうか？
①エンジンが冷えていて、メインジャーナルオイルクリアランスが小さく、クランクシャフトの回転摩擦抵抗が大きい。
②カストロールRS 10W-50が冷えていて粘度が激高くクランクシャフトの回転摩擦抵抗が大きい。
③バッテリーが上がり気味で元気がない。
④バッテリーが冷えていて元気がない。
⑤スターターモータが劣化していて元気がない。

予備のバッテリーを家から持ってきてつないだらそこそこ元気良く回ったのでたぶん③と④なのですが、①の影響を計算してみることにしました。

摩擦は直接計算できないので、オイルクリアランスの変化を計算します。

計算はシリンダブロック、ベアリングキャップ、メインベアリングの寸法および線膨張係数を下記の値として、温度別に寸法変化と常温時のオイルクリアランスから計算しました。

実際の形状やベアリングキャップボルトの影響等も考慮すべきですが、おおまかな値を知りたいだけなので今回は考慮していません。

線膨張係数
・シリンダブロック（アルミ）：2.1×10^(-5)
・ベアリングキャップ(鋳鉄)：1.1×10^(-5)
・メインベアリング（スチール）：1.1×10^(-5)
・クランクシャフト（スチール）：1.1×10^(-5)

寸法
・メインジャーナル径：Φ55
・シリダブロックジャーナル内径：Φ60
・メインベアリング肉厚：t2.5

常温(20℃)オイルクリアランス(サービスマニュアル記載値)
・17～41μm（中央29μm)

計算結果


僕のS2000の常温オイルクリアランスがいくつかわからないので、ここでは中央値と仮定すると、20℃では29μmです。(グラフの①)
エンジン始動時のエンジン温度が0℃だとすると、このときのオイルクリアランスは24μmという計算結果になりました。(グラフの②)

オイルクリアランス24μmは大きいのか小さいのか感覚的にわからないので、オイルクリアランス設定の最小値と比較します。

すると、常温の設定最小値は17μmになっているので、24μmはそんなに小さい値ではないということがわかりました。

今回の計算はあまり正確とは言えないのですが、ついでに-20℃のときを見てみます。
宇都宮では-20℃になるときはないものの、日本でも北海道では普通にありえる気温なので、-20℃でエンジン始動できないと困るはずです。

オイルクリアランス最小設定時の-20℃オイルクリアランスは7μmでした。

7μmでエンジンかかるなら、24μmだったら余裕で回ると思われます。

なので、0℃くらいであればエンジン始動時のスターターの回りが悪い原因はメインジャーナルのオイルクリアランスが小さいことが主たる理由ではなさそうだ といことが今回の計算でわかりました。

ということで、予備バッテリーを家で充電して交換したいと思います。

こんにちは。

24日のニュース見ましたか？
ニュースの見出しの多くに「ホンダF1復帰」と記載がありました。

ただ、中身を読むと2026年からも運営は変わらずHRCなので、実際は2026年以降もHRCとして参戦を継続するということと、供給チームがアストンマーチンになったという2つのことが発表されたのであって、復帰という表現は間違っていると思いました。

それにホンダはF1参戦は終了しているので、復帰することなどあり得ないのです！！。

スポンサーがホンダ(ここで言うホンダは㈱本田技研工業)というのは、かなり心配ではありますが、2026年以降もHRCがF1を継続してくれるのはうれしいですね。


さて、ホンダと言えば電動化に力を入れているわけですが、もし世の中の自動車の多くが電気自動車になったとき、だれが発電してくれるのか？東京電力は発電してくれるのか？ これが心配でなりません。

せっかく、電気自動車が普及しても、電気が足りなくてはまともに走ることができないのです。

そこで今日は、電気自動車が普及した場合、電気は足りそうなのか、なんとかなりそうなのかを大雑把に計算してみたいと思います。

まずは、1年間で使うエネルギー量を計算してみます。
僕の場合、すごく多い年で1年間に1万kmくらい走ります。

平均燃費はS2000だと8km/Lくらいなのですが、昨今のクルマはもっといいので、15km/Lということにします。

ガソリンの密度を0.78kg/Lとすれば、ガソリン1kgの燃費は
15／0.78＝19.2(km/kg)

ガソリンの低位発熱量は44MJ/kgらしいので、1km走行するために使うエネルギーは
44／19.2＝2.29(MJ/km)

1年で1万km走行するときに使うエネルギーは
2.29x10,000＝22,900(MJ)

ここで、ガソリンエンジンでは消費したガソリンの持っているエネルギーの１／３くらいしか実際の走行に使われていないので、実際の走行に使われているエネルギーは
22,900／3＝7,633(MJ)

電気自動車のエネルギー変換効率がよくわりませんが、ここでは100%ということすれば、最低でも1年間に7,633MJの電気エネルギーが必要だということがわかりました。

7,633MJ(メガジュール)ってどのくらいのエネルギーなのか見当がつかないので、わが家の電気使用量と比較してみます。

わが家は僕と奥さんの二人暮らしで、空調機もほとんど使わないのですが、半分くらい在宅勤務してるのと、テレビがプラズマなのと、奥さんが”毎日”リビングの明りを点けたまま夜中まで眠っているので、そこそこ使っているかもしれません。

そんな状態で約200kWh／月の電気を使っていました。
ということは1年で2,400kWhです。

1kWh＝3.6MJ(1000Wx3600秒)なので

1年で使う電気エネルギーをジュール換算すると
2,400x3.6＝8,640(MJ)

まとめると
1年間に自動車が使うエネルギー：7,633MJ
1年間に家庭で使うエネルギー：8,640MJ

1年間の走行距離が1万kmで、かつ燃費が15km/Lの自動車が1年間で使うエネルギーと1年間で家庭で使う電気エネルギーはほぼ同じということがわかりました。

日本の家庭のすべてが自動車を持っているわけではないこと、工場などの産業で消費する電気エネルギーが全体の約70%程度あることなどを考えると、意外になんとかなる気がしてきました。

ただ、現状でも暑い日や寒い日は電気が不足気味と言われているので、行政はこのあたりのバランスをうまく取ってもらいながら、電気不足にならないようにして欲しいですね。

それでは、寝るときは明りを消して眠りましょう！！。

今年のGWは特に用事がないので家でのんびり過ごしてます。

さて、今日は先日Garage K氏が書いていた、チューニングカー用4ローターのエキセントリックで使われているテーパ接合はなぜ滑らないのか？という疑問に対し、実際に計算をして確かめてみることにします。

とは言うものの、実際の寸法も部品構成もよくわからないので、写真を見たイメージで勝手に考えた構造、寸法でおおよその成立性を計算しました。



計算結果としてはテーパ接合の摩擦トルクは約2800Nmとなりました。
2800Nmで捩じると接合面が滑ると言う意味です。
実際はボルトの軸力、摩擦係数、テーパ部の径によって変わるのですが、仮に1／3しかなくても900Nmくらいはありそうです。

次に、このエンジンの最大発生トルクが400Nmとしたときにテーパ接合部が滑るかどうかを考えます。

実際のエンジン発生トルクは1回転中に変動があって、カタログの最大発生トルクというのは本当の最大発生トルクではなく、変動するトルクの平均値のことを言います。

グラフがあった方がわかりやすいので、自動車技術開論文集Vol.52のfig.3をご覧ください。

これは普通の4気筒のグラフで、本当の最大トルクは約300Nmになっていて、平均値はおおよそ80Nmくらいになっています。

つまり、普通の4気筒の場合は平均値の約4倍くらいの最大トルクがクランクシャフトにかかっているということになります。

今回は４ロータのエキセントリックシャフトで、1つのテーパ面は1つのロータの発生するトルクしか伝達しないため、テーパ面には400Nmの1／4の100Nmがかかります。

普通の4気筒は1回転に2回燃焼ですが、ロータリーの場合は1つのロータでは1回転で1回燃焼のため、トルク変動も4気筒の約2倍くらいあると仮定します。

したがって、100Nm×4×2＝800Nmが1つのロータで発生する最大トルクということになります。

まとめ
テーパ接合面の摩擦トルク：約900～2800Nm
ロータで発生する最大トルク　：約800Nm
摩擦トルク＞ロータで発生する最大トルク　となり、テーパ接合面は滑らず、トルクを伝達することが可能。

条件設定に仮定が多く、特にボルト軸力は怪しいところはありますが、計算上は十分成立するという結果になりました。