タツゥのブログ一覧

2012年の5月から作り始めたサーキットシミュレーションですが、少しずつ改善をしてバージョンアップをしてきたのですが、最近外にでかける元気がないので、家にこもって具合の悪いところをまとめて直しました。

直したところはたくさんあるのですが、今回もっとも力を入れたのは計算時間の短縮です。

僕のデスクトップで計算すると、ＣＰＵのパワーがあるので、鈴鹿サーキットのように計算回数の多いコースでも約３０秒で計算できるのですが、ノートパソコンで計算すると３分２０秒もかかってしまいました。

そもそも、このサーキットシミュレーションはサーキットで使うには現場向きではないのですが、１つの計算に３分もかかっていては全く使えません。
家で使う場合も１回の計算が１０秒以内で終わらないとややイラっとするので、大幅に時間短縮をしたくなりました。

僕はコンピュータのプログラムに関しては、ほとんど素人なので、いまいちわかっていないのですが、シミュレーションの計算途中を見ていると、計算と表示を交互に行うような場合に時間がかかっているように感じたので、計算を先に行ってからまとめて表示をすることにしました。

その結果、デスクトップでは３秒２、ノートパソコンでは２４秒にまで計算時間の短縮できました。
どちらも約９０％の時間短縮成功です！。

僕のブログを見て、エクセルでサーキットシミュレーションをしている人がどれだけいるのかわかりませんが、以前ブログに載せたプログラムと最新のものは変更点がたくさんあるので、改めて掲載することにしました。

今回のものは、従来に対し以下の点が異なります。
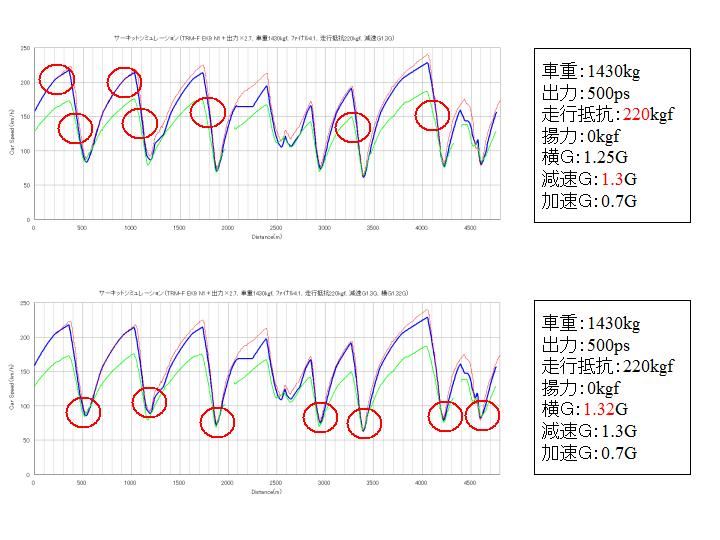
１、ダウンフォースによる横Ｇの反映
２、コースの高低差による加速度の反映
３、計算時間短縮

あとは、路面のバンク角くらいかな？

'23.09.23：Excel 2021で計算したらやたらと時間がかかったので、合計時間の表示方法変更しました。

'24.02.08：気が付いたらまた計算が遅くなっていたので原因を探ったところ、計算結果を使って、表の中に追加した計算をするときに自動計算が働いて遅くなっていました。
自動計算をオフにしたところ、元に戻ったので、VBAの中に結果を表に表示するときだけ自動計算をオフにするプログラムを追加しました。

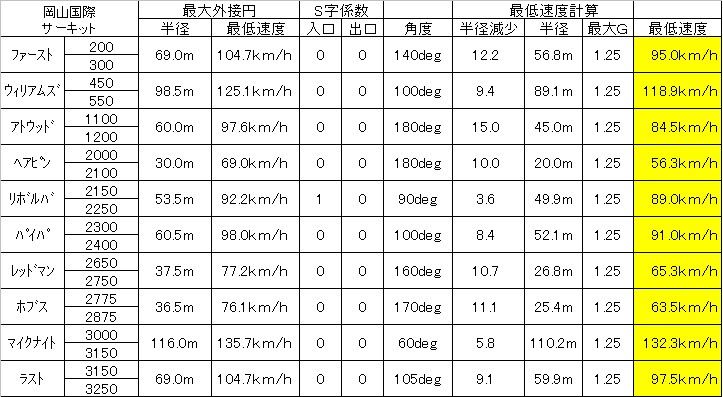
計算シート


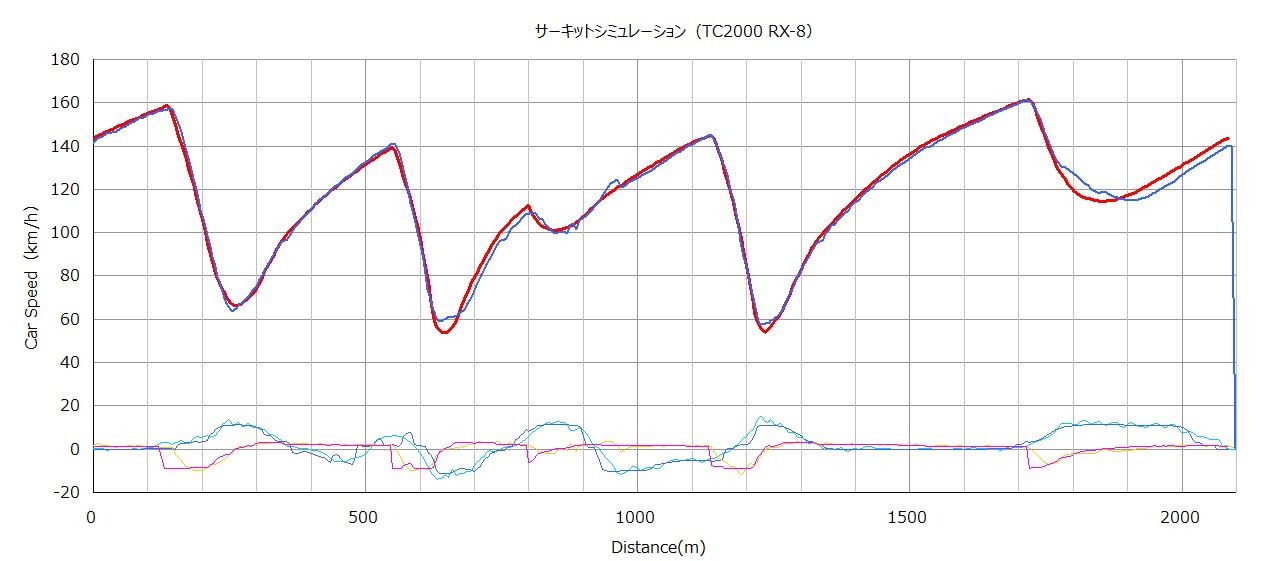
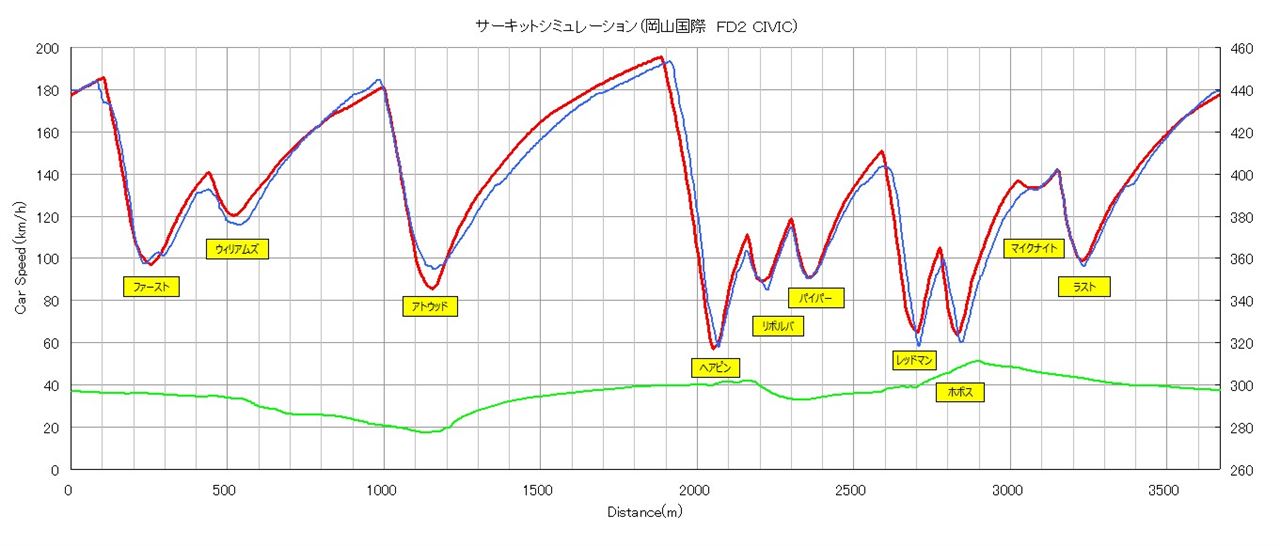
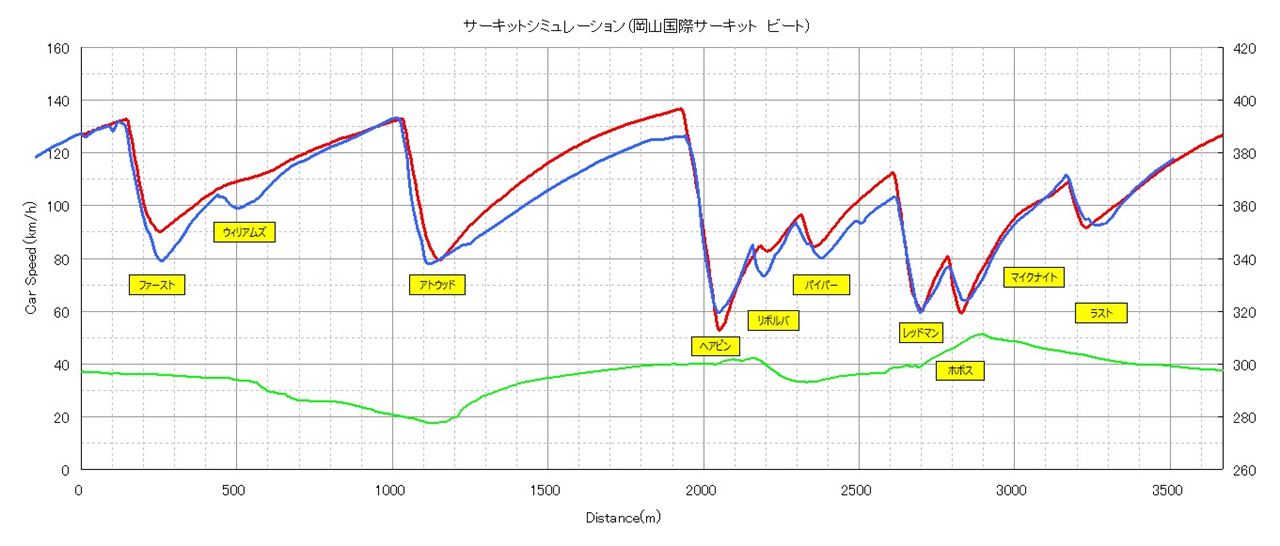
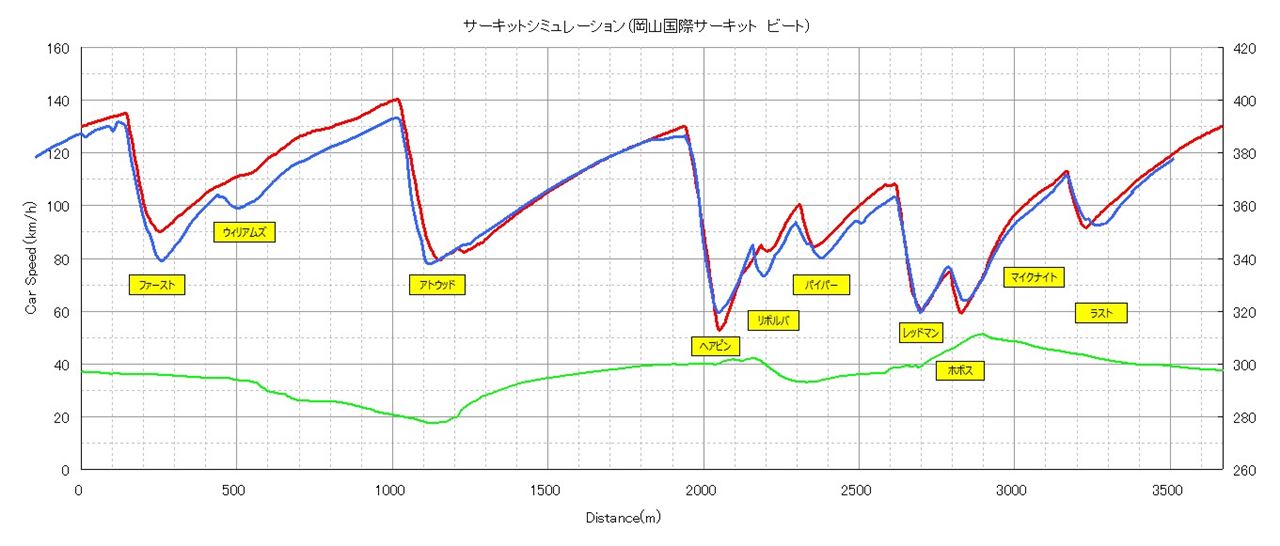
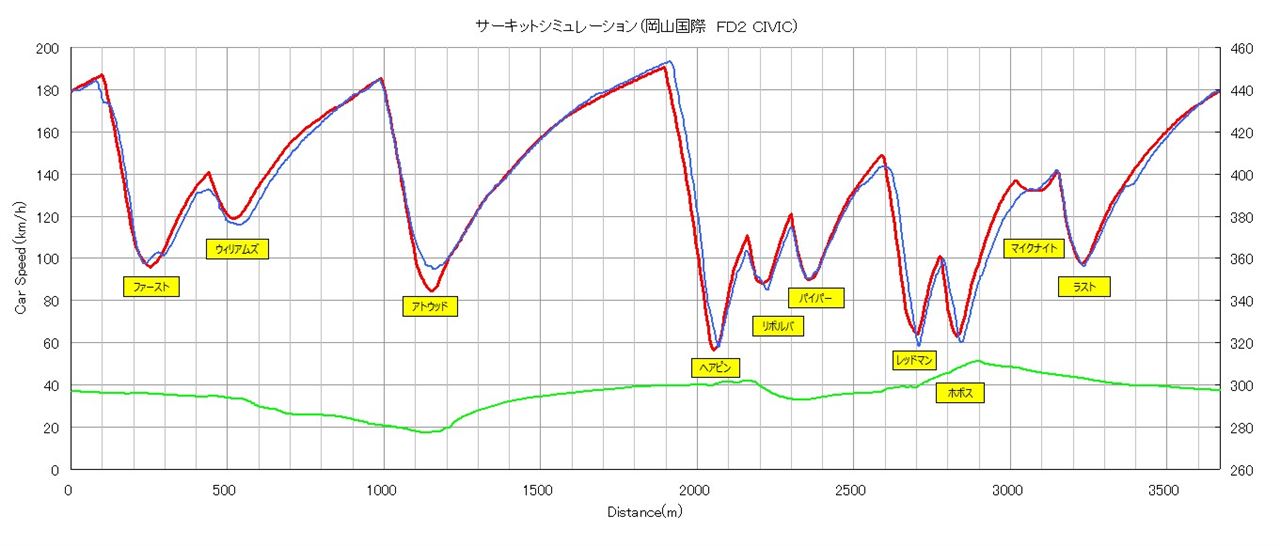
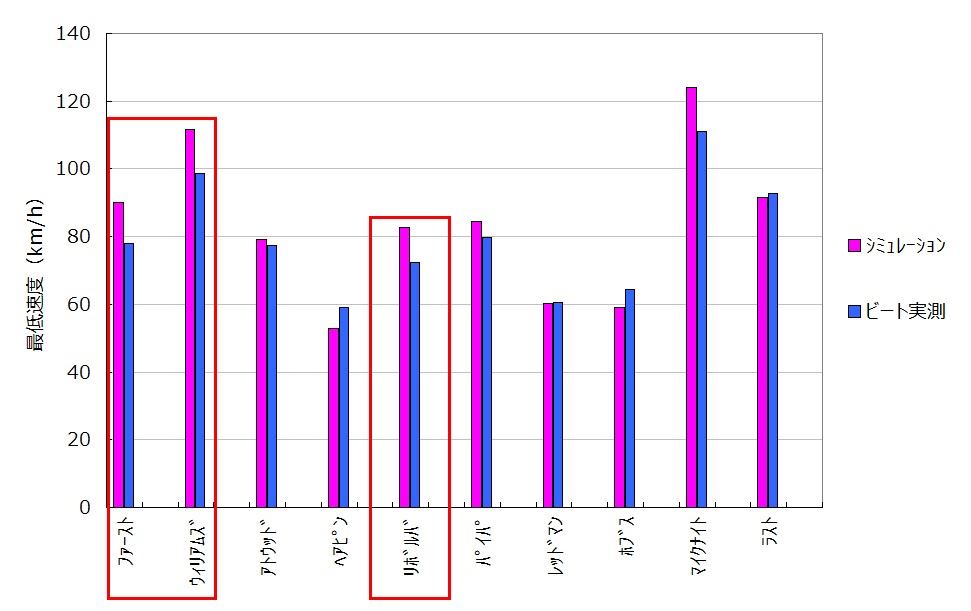
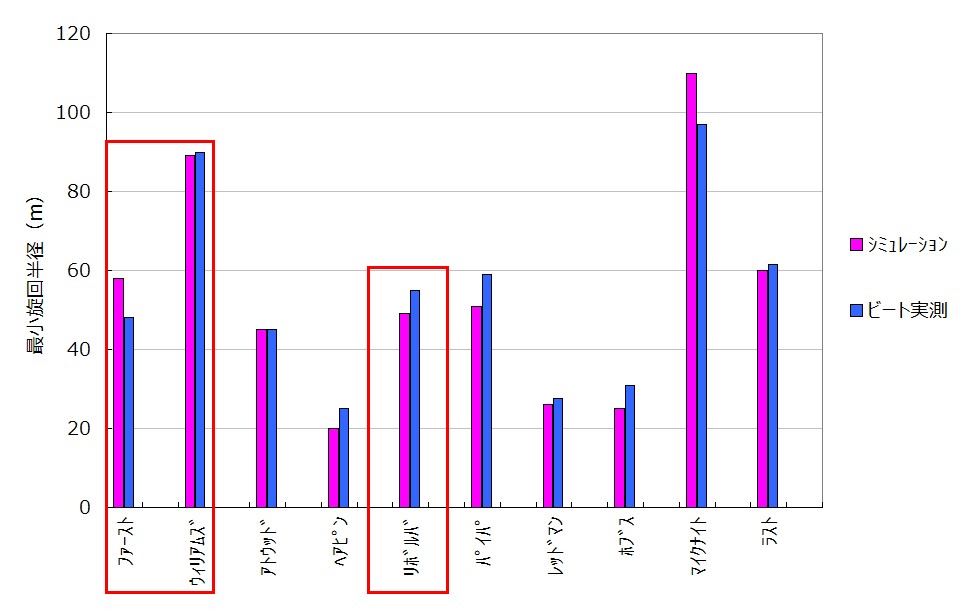
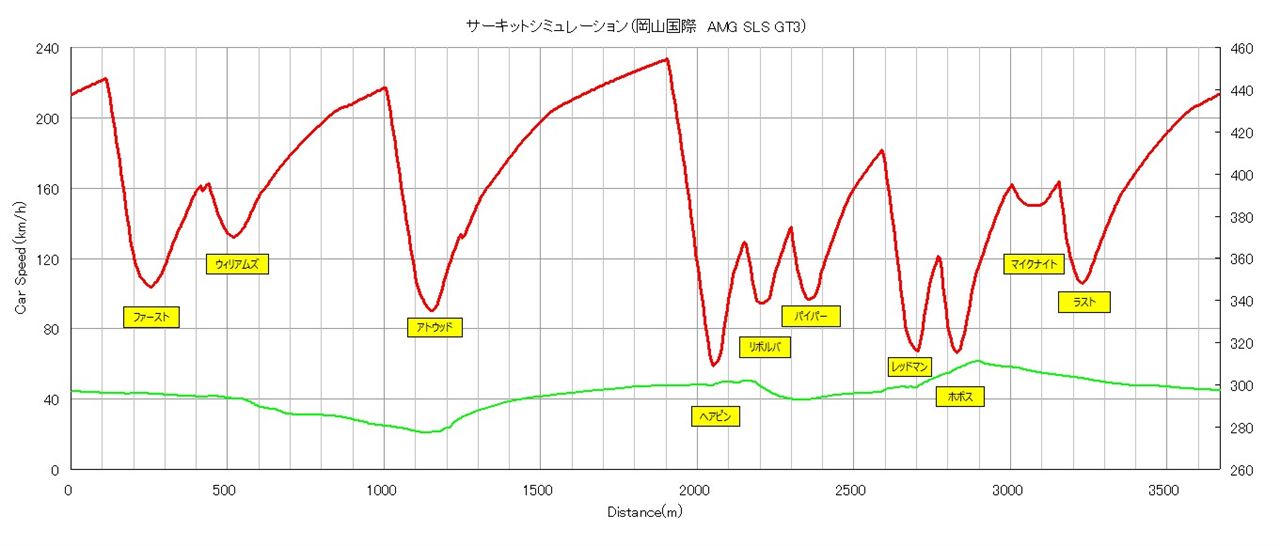
計算結果
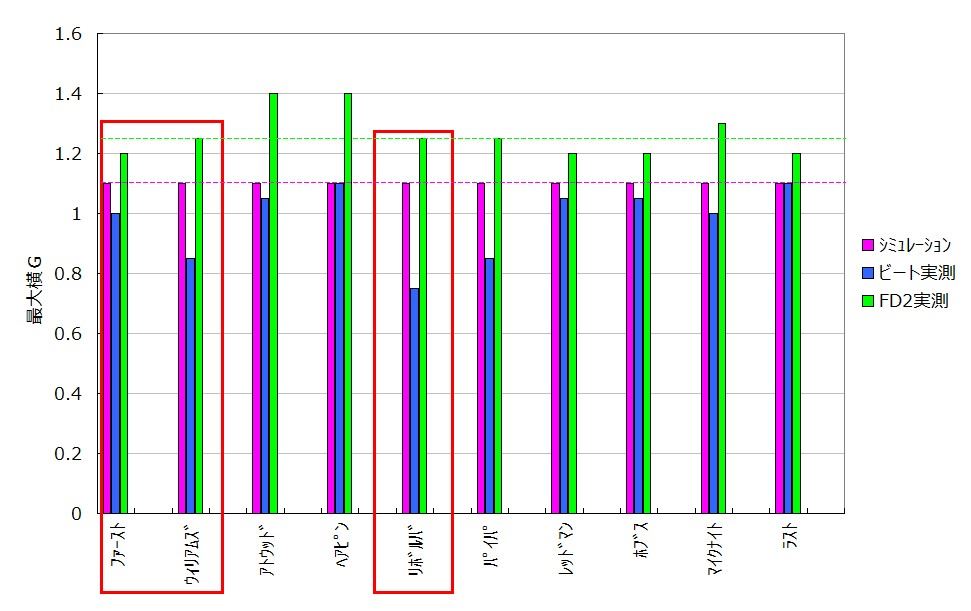
高低差を反映した結果、従来よりも実測に合うようになりました。
走行距離の違いはGPS座標から距離を算出する式を正しくした結果です。


マクロ
※行と列は計算シートに合わせてください。

Sub CircuitSim()

Dim P As Integer '計算区間数

Dim S As Integer '計算先頭行

Dim Q As Integer '計算行

Dim D As Integer 'コース分割数

Dim k As Integer '減速計算の繰り返し

Dim i As Integer '加速計算の繰り返し

Dim j As Integer '積算時間計算表示の繰り返し

Dim R As Single '曲率半径（m）

Dim H0 As Single '初期標高(m）

Dim H1 As Single '次区間標高(m）

Dim axmax As Single 'タイヤ摩擦円横Ｇ最大値

Dim aydmax As Single 'タイヤ摩擦円減速Ｇ最大値

Dim ayamax As Single 'タイヤ摩擦円加速Ｇ最大値

Dim axmaxv As Single 'ダウンフォース込みタイヤ摩擦円横Ｇ最大値

Dim aydmaxv As Single 'ダウンフォース込みタイヤ摩擦円減速Ｇ最大値

Dim ayamaxv As Single 'ダウンフォース込みタイヤ摩擦円加速Ｇ最大値

Dim ayemax As Single 'エンジン加速G最大

Dim kxg As Single '横Ｇ抵抗係数

Dim kzg As Single 'タイヤ摩擦円増加係数

Dim dX As Single '区間距離（ｍ）

Dim dT As Single '区間時間（sec）

Dim V0 As Double '初期速度（m/sec）

Dim V1 As Double '次区間速度（m/sec）

Dim VM As Single '区間中間速度（m/sec）

Dim dV As Single '速度変化量（m/sec）

Dim UT As Single 'タイヤ使用率

Dim rV As Single '速度刻み幅（m/sec）

Dim ax As Single '横加速度（G）

Dim ay As Single '前後加速度（G）

Dim dVmax As Single '計算時最大速度

Dim time As Single '積算時間(sec)

axmax = Cells(2, 2) * 9.806 '単位換算

aydmax = Cells(3, 2) * 9.806 '単位換算

ayamax = Cells(4, 2) * 9.806 '単位換算

kxg = Cells(6, 2) '横G抵抗係数読み込み

kzg = Cells(4, 13) '揚力係数読み込み

P = Cells(9, 9) '区間数読み込み

S = 15 '加速計算開始行

Q = P + S '計算行の計算

D = Cells(8, 9) 'コース分割数の読み込み

Range(Cells(S, 2), Cells(Q, 13)).ClearContents '前回計算結果の消去

Cells(Q, 2) = Cells(Q, 1)

'減速側計算

For k = 0 To P - 1

dX = Cells(Q, 16) '区間距離読み込み

V0 = Cells(Q, 2) '初期速度（最低速度）読み込み

V1 = Cells(Q - 1, 1) '次区間の横G限界速度読み込み

dV = V0 - V1 '速度増加量の計算

R = Cells(Q - 1, 15) 'コーナ曲率半径読み込み

H0 = Cells(Q, 18) '初期標高読み込み

H1 = Cells(Q + 1, 18) '次区間標高読み込み

dH = H1 - H0 '区間高低差計算：正は上り

aH = 9.806 * dH / (dX ^ 2 + dH ^ 2) ^ 0.5 '高低差による加速度計算

If dV >= 0 Then '速度変化が正のとき:加速時

Cells(Q - 1, 2) = V1 '次区間速度V1をシートに入力

'速度変化が負のとき：減速時

Else

UT = 2 'タイヤ使用率を2とする

aydmaxv = aydmax * (1 + kzg * V1 ^ 2) + aH 'ダウンフォース込み減速加速度最大値計算

dVmax = (-V0 + (V0 ^ 2 + 2 * aydmaxv * dX) ^ 0.5) '最大減速可能量を計算

Do Until UT <= 1 'タイヤ使用率が1以下になるまで繰り返し

dV = V0 - V1 '速度変化量計算：正は加速

VM = (V0 + V1) / 2 '区間中間速度計算

dT = dX / VM '区間時間の計算

ay = dV / dT '減速加速度計算

ax = V1 ^ 2 / R '横加速度計計算

aydmaxv = aydmax * (1 + kzg * V1 ^ 2) + aH 'ダウンフォース込み減速加速度最大値計算

axmaxv = axmax * (1 + kzg * V1 ^ 2) 'ダウンフォース込み横加速度最大値計算

UT = ((ax / axmaxv) ^ 2 + (ay / aydmaxv) ^ 2) ^ 0.5 'タイヤ使用率計算

If dV >= 0 Then '速度変化量が正のとき（加速時）

UT = 1 'タイヤ使用率を1とする

End If

If Abs(dV) > dVmax Then '速度変化量が最大減速可能量よりも大きい場合

rV = Abs(dV) - dVmax '速度刻み幅計算

Else

rV = dVmax / 100 '速度刻み幅計算

End If

Cells(Q - 1, 2) = V1 'シートに次区間速度を入力：速度の確定

V1 = V1 - rV '次区間速度計算

Loop

Cells(Q, 3) = dV 'シートに速度変化量を入力：結果確認用

Cells(Q, 4) = dT 'シートに区間時間を入力：結果確認用

Cells(Q, 5) = ax 'シートに横加速度を入力：結果確認用

Cells(Q, 6) = ay 'シートに減速加速度を入力：結果確認用

UT = ((ax / axmaxv) ^ 2 + (ay / aydmaxv) ^ 2) ^ 0.5 'タイヤ使用率計算

Cells(Q, 7) = UT 'シートにタイヤ使用率を入力：結果確認用

End If

Q = Q - 1

Cells(9, 7) = Q

Next k



'加速側計算

Q = S '計算開始行

For i = 0 To P - 1

dX = Cells(Q + 1, 16) '区間距離読み込み

V0 = Cells(Q, 2) '初期横G限界速度読み込み

V1 = Cells(Q + 1, 2) '次区間速度計算

dV = V1 - V0 '速度変化量計算：正は加速

R = Cells(Q + 1, 15) 'コーナ曲率半径読み込み

H0 = Cells(Q, 18) '初期標高読み込み

H1 = Cells(Q + 1, 18) '次区間標高読み込み

dH = H1 - H0 '区間高低差計算：正は上り

aH = 9.806 * dH / (dX ^ 2 + dH ^ 2) ^ 0.5 '高低差による加速度計算

If dV <= 0 Then '速度変化量が負のとき（減速時）

Cells(Q + 1, 2) = V1 '次区間速度をV1とする

Else '速度変化量が正のとき（加速時）

Cells(Q, 3) = dV 'シートに速度変化量を入力：結果確認用

VM = (V0 + V1) / 2 '区間中間速度計算

dT = dX / VM '区間時間計算

ay = dV / dT '加速度計算

ayemax = Application.WorksheetFunction.Lookup(V0, Worksheets("Power").Range("I36:I3336"), Worksheets("Power").Range("H36:H3336"))

'エンジン加速度をpowerシートから参照

Cells(Q, 8) = ayemax 'シートにエンジン加速度を入力


If ay > ayemax - aH Then '加速度がエンジン加速度よりも大きい場合

ax = V0 ^ 2 / R '横加速度計算

ay = ayemax - aH - Abs(ax) * kxg '加速度の計算：エンジン加速度からタイヤ抵抗を減算

dT = (-V0 + (V0 ^ 2 + 2 * ay * dX) ^ 0.5) / ay '区間時間計算

End If

'加速度がエンジン加速度よりも小さい場合

dVmax = ay * dT '最大速度変化量計算

V1 = V0 + dVmax '次区間最大速度計算

Cells(Q + 1, 2) = V1 '次区間速度をシートに入力

UT = 2 'タイヤ使用率を2とする

Do Until UT <= 1 'タイヤ使用率が1以下になるまで繰り返し

dV = V1 - V0 '速度変化量計算

VM = (V0 + V1) / 2 '区間中間速度計算

dT = dX / VM '区間時間計算

ay = dV / dT '加速度計算

ax = V1 ^ 2 / R '横加速度計算

ayamaxv = ayamax * (1 + kzg * V1 ^ 2) 'ダウンフォース込み減速加速度最大値計算

axmaxv = axmax * (1 + kzg * V1 ^ 2) 'ダウンフォース込み横加速度最大値計算

UT = ((ax / axmaxv) ^ 2 + (ay / ayamaxv) ^ 2) ^ 0.5 'タイヤ使用率計算

If dV <= 0 Then '速度変化量が負のとき（減速時）

UT = 1 'タイヤ使用率を1にする

End If

'速度変化量が正のとき（加速時）

V1 = V1 - dVmax / 100 '次区間速度計算

Cells(Q + 1, 2) = V1 '次区間速度をシートに入力

Loop

Application.Calculation = xlCalculationManual '手動計算

'結果表示

Cells(Q, 3) = dV 'シートに速度変化量を入力

Cells(Q, 4) = dT 'シートに区間時間を入力

Cells(Q, 5) = ax 'シートに横加速度を入力

Cells(Q, 6) = ay 'シートに加速度を入力

UT = ((ax / axmaxv) ^ 2 + (ay / ayamaxv) ^ 2) ^ 0.5 'タイヤ使用率計算

Cells(Q, 7) = UT 'シートにタイヤ使用率を入力

End If

Q = Q + 1

Cells(8, 7) = Q

Next i


'結果計算 1ｺｰﾅ最低速度まで

Q = S '計算開始行

For j = 0 To P - D

If Cells(Q, 2) > Cells(Q + D, 2) Then '減速時速度が低いとき

Cells(Q, 9) = Cells(Q + D, 2) * 3.6 'シートに速度を入力

Cells(Q, 11) = Cells(Q + D, 5) 'シートに横加速度を入力

Cells(Q, 12) = Cells(Q + D, 6) 'シートに前後加速度を入力

Cells(Q, 13) = Cells(Q + D, 7) 'シートにタイヤ使用率を入力

Else:

Cells(Q, 9) = Cells(Q, 2) * 3.6 'シートに速度を入力

Cells(Q, 11) = Cells(Q, 5) 'シートに横加速度を入力

Cells(Q, 12) = Cells(Q, 6) 'シートに前途加速度を入力

Cells(Q, 13) = Cells(Q, 7) 'シートにタイヤ使用率を入力

End If

Q = Q + 1

Next j

'結果計算 1ｺｰﾅ最低速度からｺﾞｰﾙまで

Q = P - D + S '計算開始行

For j = 0 To D

Cells(Q, 9) = Cells(Q, 2) * 3.6 'シートに速度を入力

Cells(Q, 11) = Cells(Q, 5) 'シートに横加速度を入力

Cells(Q, 12) = Cells(Q, 6) 'シートに前途加速度を入力

Cells(Q, 13) = Cells(Q, 7) 'シートにタイヤ使用率を入力

Q = Q + 1

Next j

'結果表示 合計時間

P = Cells(9, 9) '区間数読み込み

Q = S '計算開始行

Cells(Q, 10) = 0

For j = 0 To P - 1

Q = Q + 1

Cells(Q, 10) = Cells(Q - 1, 10) + Cells(Q, 16) / Cells(Q, 9) * 3.6 'シートに積算時間を入力

Next j

Application.Calculation = xlCalculationAutomatic '自動計算

End Sub

今日は、シャア少佐から「連邦軍のモビルスーツがきさまのいうとおりの性能とはやや信じがたい」とあまり信用されていない、スレンダーさんの走行データを見てみます。

では、まずシミュレーションとの比較を見てみましょう。
青：実測、赤：シミュレーション


シミュレーションの条件
最大横Ｇ：１．１５
最大減速Ｇ：０．９３
最大加速Ｇ：０．６５
出力補正：０．７５

ラップタイム
実測　　　　　　　：１分０８秒１５５
シミュレーション：１分０８秒３７

なんと！、シミュレーションよりも速いです。
原因は、TC2000の場合、１ヘアと２ヘアにバンク角がついているので、その分高い横Ｇが発生できるのですが、シミュレーションでは１コーナ、ダンロップ、最終コーナでおおよその合わせ込みをするため、全体的にうまく走れている場合、シミュレーションの方が遅いタイムになります。

そして、グラフの比較を見ると、全ての場所においてシミュレーションとの差が小さいことがわかります。

このことが意味することは

１、ブレーキはどこのコーナでもしっかり踏めている
２、どこのコーナもタイヤのグリップを使いきって（摩擦円の縁に沿って）走ることができている
３、走行ラインの旋回半径がシミュレーションとほぼ同じ

ということで、大ざっぱに見ると、これと言って具合の悪いところは見当たりません。

強いて上げると、１ヘアと最終コーナはシミュレーションとの差が見られます。
しかし、このくらいの差になると、そもそもシミュレーションが正しくできているか？ということを検証する必要があるので、次回から順番に見ていきたいと思います。

暑い、暑い、暑い～～！！
にもかかわらず、朝起きたら空調機が不調です。
数年前から不調なのですが、ごまかしながら使っています。

今日はしばらくガマンしていましたが、暑さでどうにもならなくなってきたので、昨年発見した”エアコン洗浄スプレーをセンサに吹き付けると復活する”という技で今回もごまかしました。

さて、今日のお題ですが、岡山国際サーキットです。
mistbahnさんが岡山国際サーキットを走行されたというブログがあっていたので、以前の日光サーキットのシミュレーション条件を用いてシミュレーションしてみました。

まずは、岡山国際サーキットのコーナ名をおぼえなければなりません。
コース図はこちらから入手してください。

次は僕の手持ちのデータで走行ラインの作成と合わせ込みを行います。
クルマはスリックタイヤのFD2シビックです。

合わせ込みの結果
赤がシミュレーションで青が実測です。


岡山国際は高低差影響が大きいので、今回はグラフにロガーのhight（標高）を緑の線で表示しています。（岡山国際のコース図に記載してあるものと比較してもそこそこ合ってます）

アトウッド～ヘアピンの直線部に差がある原因は、コースが上りになっていることだということがわかります。

コーナの最小半径は、実測ではなく推奨値を使いました。


推奨値の計算表の中にＳ字係数という意味深な言葉がでてくるのですが、このＳ字係数は、文字通りＳ字状のコーナでの半径減少量計算で使います。
過去の実測データから、Ｓ字の場合は半径減少をしない場合が多いので、入り口だけなら半径減少を半分にして、入り口と出口の両方の場合は半径減少量を０にします。

しかしながら、Ｓ字の事例が少ないのでいまいちまだよくわかっておらず、今回はヘアピン～リバルバのリボルバだけに適用しました。

そこそこ実測とシミュレーションが合ったので、ビートでシミュレーションしました。
ラップタイムは２分１１秒１４です。
赤がシミュレーションで青がmistbahnさんの実測です。


岡山は全体的にコーナにバンク角がついているので横Ｇは前回の１．０Ｇから１．１Ｇにしています。
また、前回と同じ条件では直線加速部がいまいち合わないので、出力補正係数を０．７５から０．７に変更しています。

しかし、アトウッド～ヘアピンの直線加速がまるっきり合いません。
そこで、コースの勾配を考慮した計算に修正しました。

修正方法は、重力加速度×勾配をエンジン出力による加速度から引くだけです。

たとえば、５ｍ進んで０．１ｍ上るような勾配の場合は
９．８０６×０．１／（５＾２＋０．１＾２）＾０．５＝０．１９６（ｍ／ｓｅｃ２）を引きます。

この修正を行った計算でシミュレーションした結果がこちらです。
ラップタイムは２分１２秒４３です。


アトウッド～ヘアピンの上り区間はおおよそ合いました。
その代わり、ウィリアムズ～アトウッドの下り区間が合わなくなりました。
しかし、ウィリアムズコーナの速度を見ると、ここの差が直線に影響しているだけなので、シミュレーション結果としては問題なさそうです。

同様にFD2シビックでも勾配を考慮してシミュレーションしました。


全体的に合うようになりました。
ホブス～マイクナイトがいまいち合わないのですが、原因不明です。


シミュレーションもそこそこうまくできていると思うので、mistbahnさんの走行データとの比較をしてみましょう。

まずはコーナ中の最低速度を比較します。

ファースト、ウィリアムズ、リボルバの３つの差が大きいのでここの原因を確認しましょう。
ちなみにマイクナイトも差が大きいのですが、マイクナイトはビートの場合、タイヤの限界で決まるコーナリング速度よりも実際に到達できる速度の方が低いので、その分だけ横Ｇが低くなっています。

コーナ中の最低速度は、最小旋回半径と最大横Ｇの２つのみで決まるのでこの２つを確認します。

最小旋回半径


ファーストはややシミュレーションより旋回半径が小さくなっています。
ウィリアムズはほぼ同じ。
リボルバはシミュレーションより少し大きいです。

最大横Ｇ
参考にＦＤ２の実測も載せました。


ファーストはやや最大横Ｇが小さいです。
ウィリアムズは最大横Ｇが０．８５Ｇしかでておらず、シミュレーションの１．１Ｇと比較すると大幅に低いです。
リボルバは０．７５Ｇしか出ていません。
ついでにその次のパイパも０．８５Ｇです。

路面的横Ｇが出にくいのかと言うと、ＦＤ２の実測結果を見てわかるように、ウィリアムズもリボルバもパイパも他のコーナと同等の横Ｇが出ているので路面の問題は考えにくいです。

横Ｇの低い３つのコーナの共通点を考えます。
１、直角コーナ
２、手前の減速区間が短い

特にウィリアムズとリボルバは、シミュレーション見るとわかるように、強い減速が不要です。
アクセルをパーシャルか、ややアクセルオフにして、とりゃあ～ってハンドル切れば曲がれるはずです。
しかし、減速をしてから曲がっているためにその分だけ横Ｇが減少していると考えられます。

減速しないと荷重移動がないので、その分曲がりずらいとは思うのですが、ビートの場合は僕の推奨値は無視して、コーナで取れる最大の先回半径で曲がった方が、最大Ｇも高くなって速く走れると思われます。


その他のコーナではアトウッドが気になります。
FD2のシミュレーションと実測の比較を見ると、実測の方が１０ｋｍ／ｈ程度最低速度が高くなっています。
この原因は、アトウッドのバンク角が大きいためだと考えられ、横Ｇは１．４Ｇも出ています。
他のコーナは１．２５Ｇ前後ですから、１２％も高い横Ｇが発生しています。

しかし、mistbahnさんの実測を見ると、アトウッドの横Ｇが１．０５Ｇと他と比べて高くありません。
恐らく１．１５～１．２Ｇは出るはずです。

ヘアピンも同様なのですが、恐らく自分の中で横Ｇの最大を決めてしまい、それ以上の横Ｇが発生するような速度で走っていないだけだと思うので、もっと速度を上げる必要があると思います。

それと、前回の日光でも書いたのですが、減速Ｇが低すぎるのが気になります。
今回のシミュレーションも０．６３Ｇを最大減速Ｇとしていますが、明らかに低いです。

走行データを見ると、減速開始からほぼ最大減速Ｇが発生できていて運転に問題は見られないのですが、０．６３Ｇではどうにもならないので、まずは減速Ｇが低い問題について対策が必要と思われます。

ということで、岡山国際のシミュレーションでした。
残る国内の大きいサーキットはＳＵＧＯとオートポリスだけになりました。
そのうち取り組みたいと思います。


追記
S耐のＡＭＧ ＳＬＳ ＧＴ３もシミュレーションしてみました。
条件は富士、もてぎと同じです。


シミュレーションのラップタイム：１分３２秒７０
２０１３年のＳ耐予選タイム　 　：１分３１秒０８７

ということで、そこそこ合ってることが確認できました。

今日は棚から一掴みのコーナです。

もてぎチャンピオンカップのような参加型レースに参戦する人は、僕の知るところではだいたい１２月くらいから練習を始めて３月末くらいに開催される第一戦に参戦するのが一般的です。

練習を始めたころは、どんどん上達するのでタイムが上がるのですが、春が来るころには上達度合いが鈍ってきます。

さらに、冬の終わりとともに気温が上昇するので、エンジンパワーが低下し、むしろラップタイムが落ちてしまう場合があります。

こんなとき、ロガーを使っていれば、直線加速が悪くなったことがラップタイム低下の原因であることは３秒でわかるのですが、使っていないと原因がはっきりしません。

また、ロガーを使っていたとしても、気温影響によるラップタイム変化を予測するためにはサーキットシミュレーションなどを使う必要があり、あまり現場向きとは言えません。

そこで、こんなときのために、僕の蓄積したデータから独自の計算手法により算出した気温係数を使ったラップタイム予測手法を紹介します。
ついでに、車重の影響も計算できる車重係数も紹介します。

ただし、コースはもてぎ、クルマはシビックＥＫ９、タイヤはＳタイヤを基準としているので、それ以外のコースやクルマにはそのまま当てはまらないと思います。

気温係数と車重係数は以下の値を使います。

　気温係数：０．０２５秒／℃／ｋｍ
　
　車重係数：０．００７秒／ｋｇ／ｋｍ

この二つの係数を基準となるラップタイムを出したときの気温と車重の差にかけることで、予測したい条件のラップタイムを算出することができます。

それでは具体事例で計算してみましょう。

コース長：４．８ｋｍ
基準タイム：１３５．１３３秒
気温：７℃、車重：８９５ｋｇ

予測したい条件
気温：２４℃、車重：９２０ｋｇ


予測タイム＝基準タイム＋気温係数×気温差×コース長＋車重係数×車重差×コース長
　　　　　　　＝１３５．１３３＋０．０２５×（２４－７）×４．８＋０．００７×（９２０－８９５）×４．８
　　　　　　　＝１３５．１３３＋２．０４＋０．８４
　　　　　　　＝１３８．０１秒

実際のタイムは、１３７．９６３秒だったので、よい精度で予測できました。

どちらも覚えずらいので
　気温に対するラップタイム変化は
　１ｋｍのコースで４℃変化すると０．１秒の変化

　車重に対するラップタイム変化は
　４．８ｋｍのコースで３ｋｇ変化すると０．１秒の変化

と覚えてください。

今まで何度も計算したことがありますが、計算値と実測が合わないこともありました。
そういう場合は、やはりロガーデータをしっかり確認したり、他のクルマのラップタイムを確認することが大事だと思います。

それと、Ｓ２０００でＴＣ１０００を走った場合、気温差が１６℃くらいあってもラップタイム変化は０．１～０．２秒程度であり、０．４秒も変化があることはないと思うので、ＴＣ１０００だと当てはまらないようです。

Ｆ１オーストラリアＧＰ面白かったですね！
それにしても可夢偉は残念！！
やっぱりブレーキバイワイヤとか信用なりませんなぁ。

昨日の合わせ込みの説明ではわかりずらかったと思うので、順番にグラフを作ってみました。

赤：ＳＬＳ ＡＭＧ ＧＴ３（これが合わせ込みの対象）、青：シミュレーション、緑：ＥＫ９シビック

①上段：まずはべースのシビックと相関が取れていることを確認します。
②下段：車重とギア比を決め、加速カーブを見ながらパワー補正値を調整します。
　車重は実際の値か推測値を使います。
　ギア比は最高速＋５ｋｍ／ｈくらいまでカバーできればなんでもよいです。
　今回は４．７８５から４．１に変更して富士の最高速２６７ｋｍ／ｈまで対応できるようにしました。


③上段：最高速を見ながら走行抵抗合わせ、減速カーブを見て減速Ｇを調整します。
もてぎのダウンヒルストレートのように、下っているところは加速カーブが合わないので、平坦なところで合わせます。
ダウンフォースの効いているクルマの場合、揚力設定０の時点では高速部の減速カーブが合わないので、そこは揚力設定時に確認します。
④下段：最低速度に着目し、横Ｇを調整します。
路面のバンク角影響を受けるため、バンク角が小さいところで合わせます。


⑤上段：中高速コーナを見て揚力を調整します。
⑥下段：低速コーナ立ち上がりを見て、加速Ｇを合わせます。


予め走行ラインが出来上がっている場合は、上記のように簡単に各数値を合わせ込むことが可能なのですが、走行ラインの合わせ込みが十分でない場合は、一度各数値の合わせ込みをおおよそ行って、その状態で走行ラインを調整し、再度各数値の合わせ込みをするという繰り返し作業になります。

実際に合わせ込みをすると、設定値を変えてもほとんど変化がない場合があります。
特に加速Ｇはあまり変化しないので走行ラインで調整すべきか、加速Ｇで調整すべきか悩ましいところです。
しかし、走行ラインは車載映像から大体のラインがわかるので、走行ラインを正として、加速Ｇを調整するのがわかりやすいと思います。

補足：走行抵抗は１８０ｋｍ／ｈ、揚力は１００ｋｍ／ｈでの値です。