



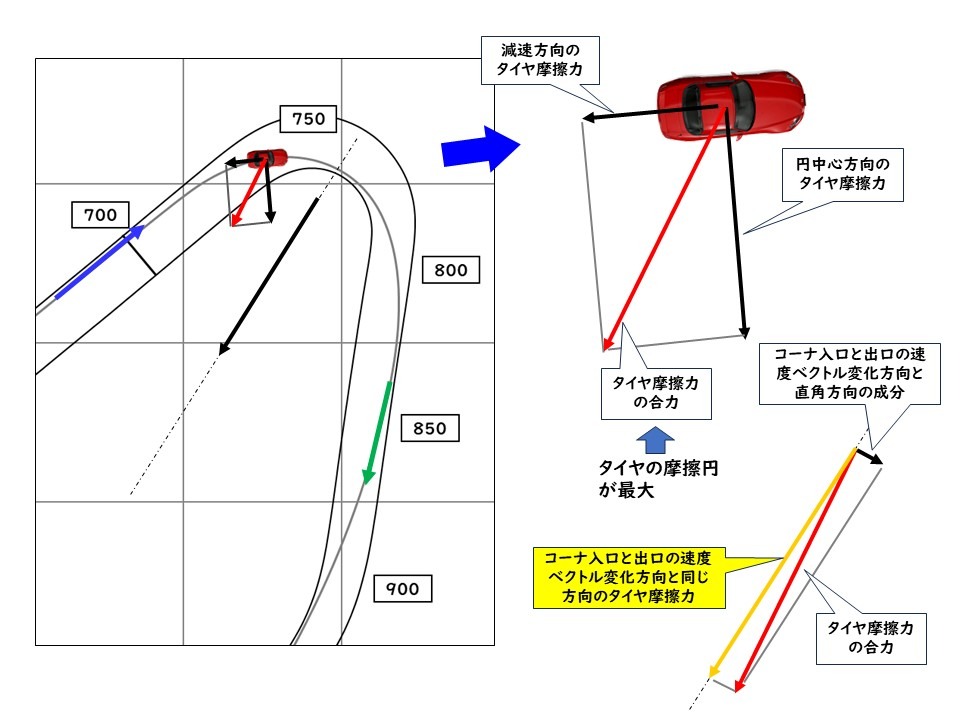

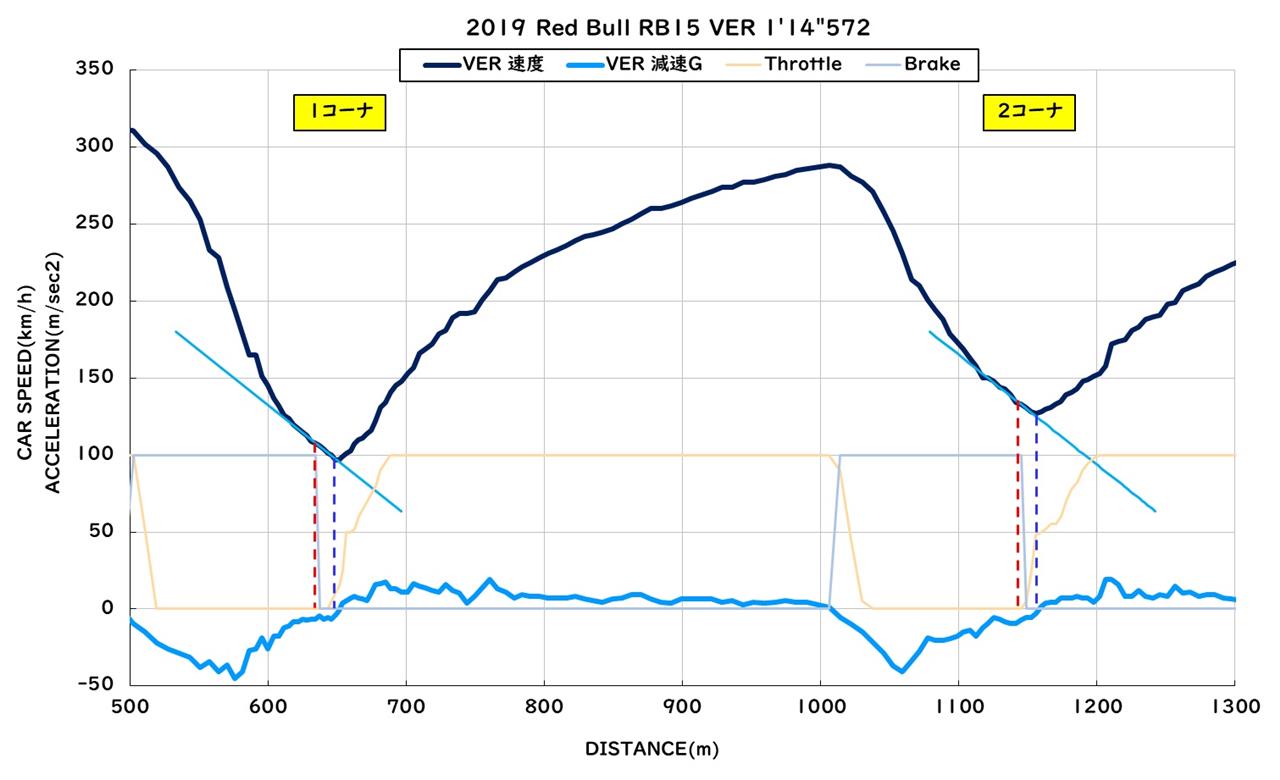



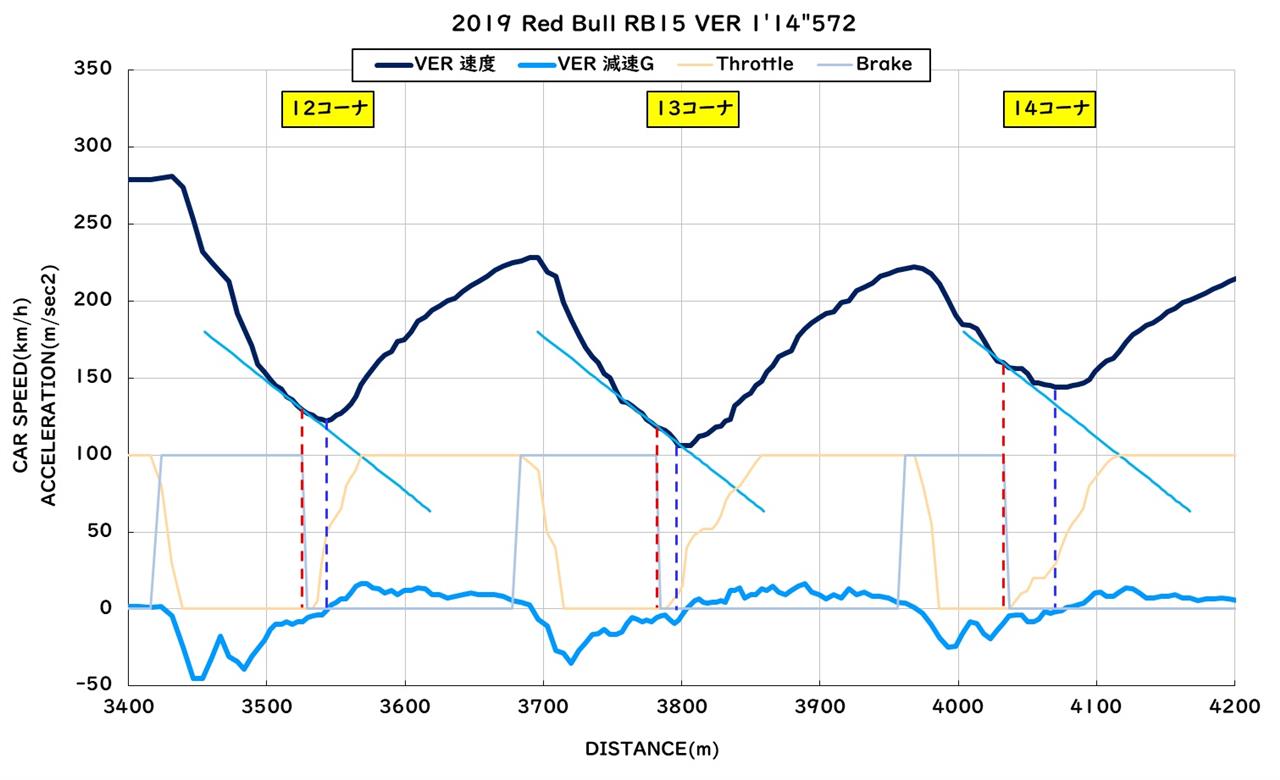

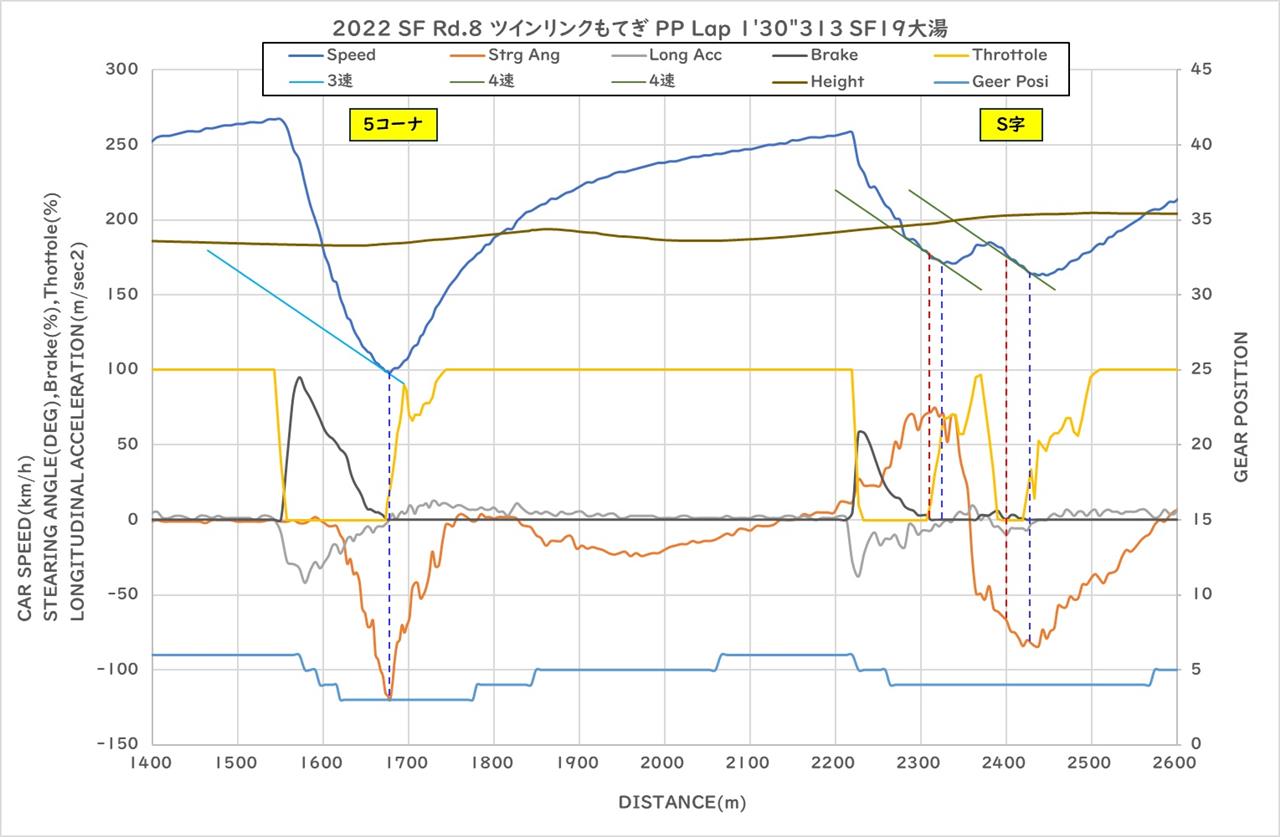

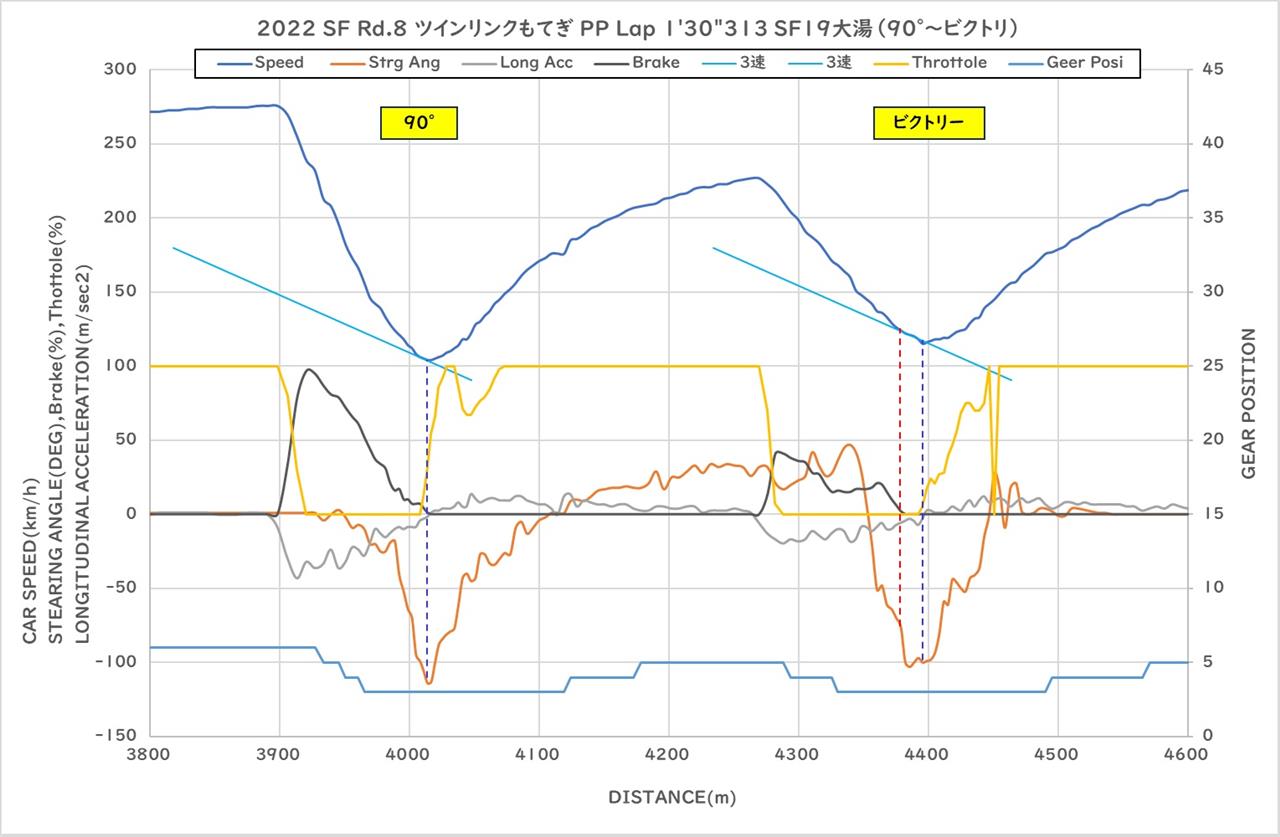
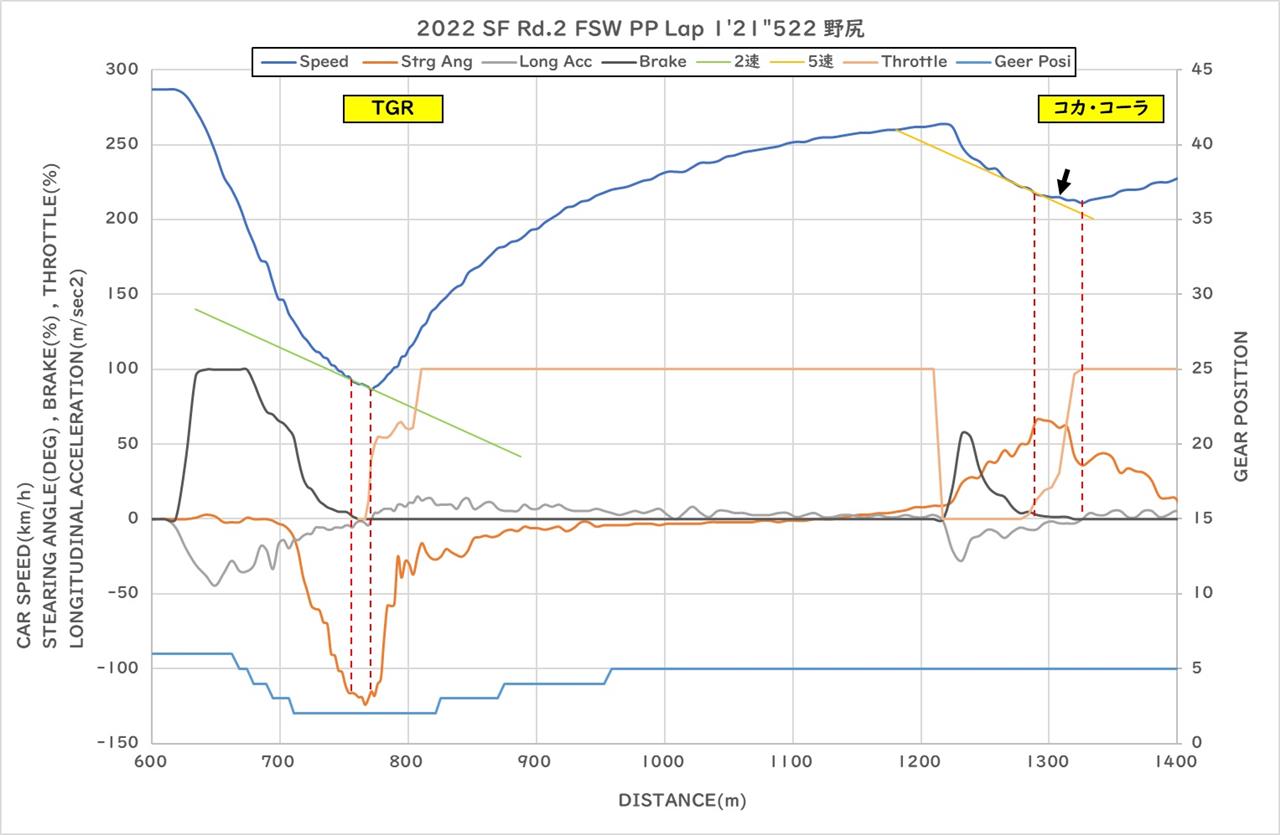


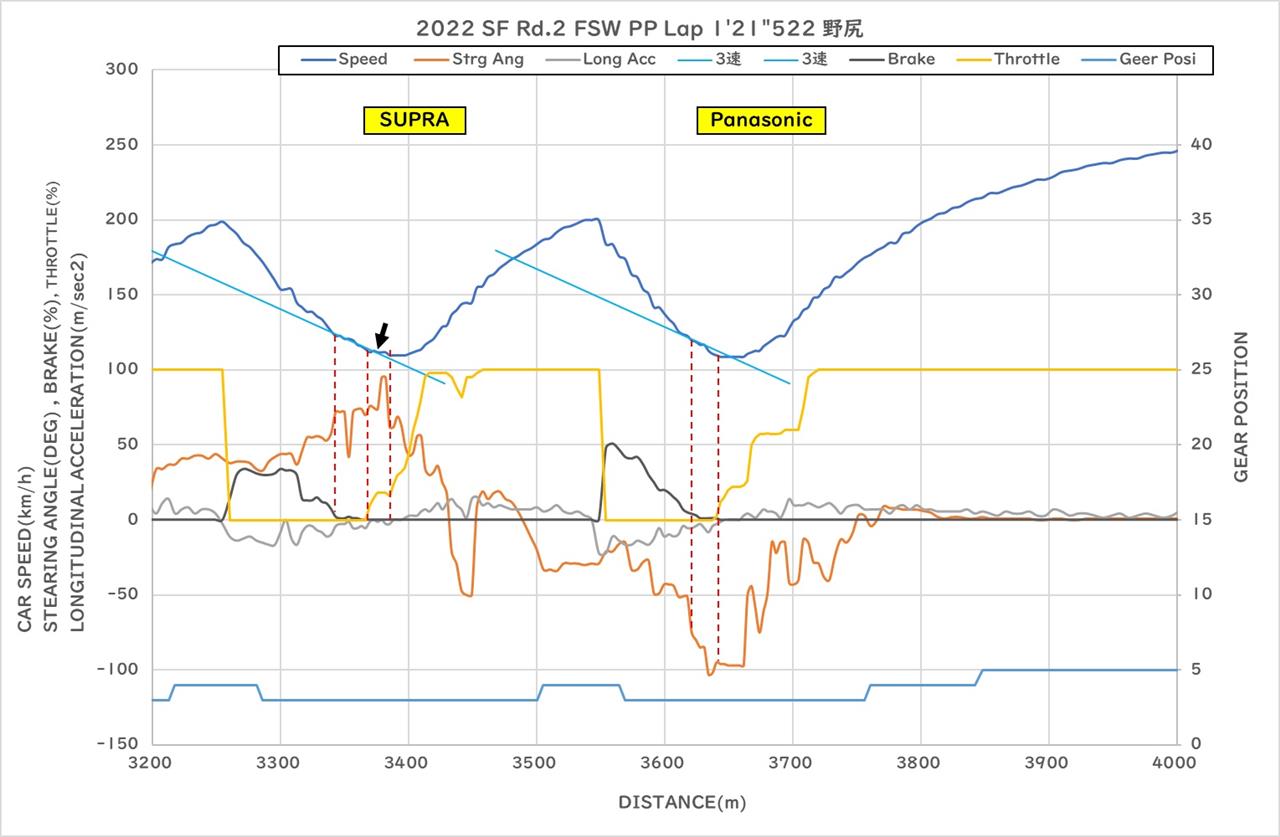
 |
ホンダ S2000 最新型のS2000が欲しくなったので買い替えました。 |
 |
アウディ A3 プレミアムコンパクトです。 コンパクトなのにプレミアム プレミアムなのにコンパクト マ ... |
 |
日産 180SX いまいち乗っていた記憶がないのですが、いい車でした。 だけど、いろいろやっていたらしい ... |
 |
日産 フェアレディZ バツグンのカッコよさを誇るZ31です。 電動ファンがいまいちだったせいか、ラジエータの冷 ... |
| 2025年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2024年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2023年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2022年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2021年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2020年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2019年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2018年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2017年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2016年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2015年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2014年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2013年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2012年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |