ゴールデンウイークも終わりが近づいてきた今日この頃、いかがお過ごしでしょうか。
僕はおととい、スカイツリー台湾祭りとお台場オクトーバーフェストをはしごしたあと、ガンダムファクトリーへ行ってきました。
それ以外はほとんど走行ライン最適化について考えることとサーキットシミュレーションの修正をひたすらしています。
なぜサーキットシミュレーションの修正をしていたかと言うと、今回の検討をするにあたり、いろんな指標で比較をする必要があり、真面目に見ていたら不具合が見つかったためです。
いずれの不具合も今までのシミュレーション結果が逆転するようなことはなかったのですが、減速Gの計算に走行抵抗が考慮されておらず、タイヤの摩擦力のみで減速しているという不具合がありました。
今までもフォーミュラカー等の高速で走るクルマの減速区間が実測と合わないという事実は認識していたものの”そういうこともある”くらいの感覚で考えてました。
減速Gの計算に走行抵抗考慮したら、かなり実測結果に近づいてきたので、今後は考慮することにしましたが、今回の説明では考慮しない方がわかりやすいので、以前のバージョンで計算してます。
したがって減速区間は摩擦円半径設定が1.0Gの場合、最大でも1.0Gでしか減速していないので、今までと今回のシミュレーション結果については”減速区間は走行抵抗がない”という前提で見てください。
そんなわけで、今日は第3回目です。
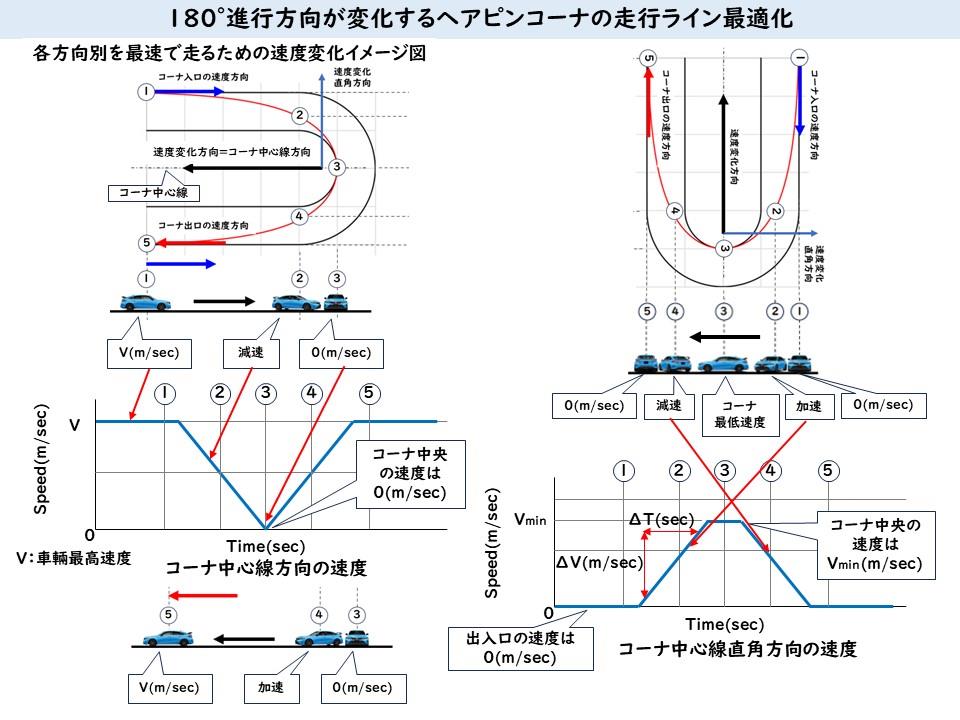
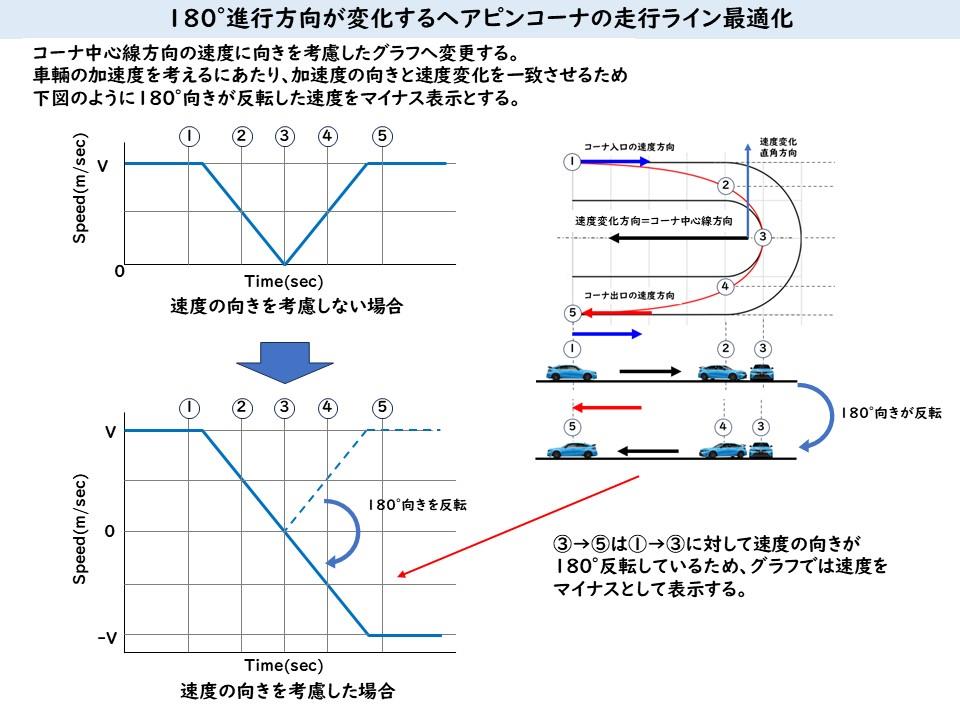
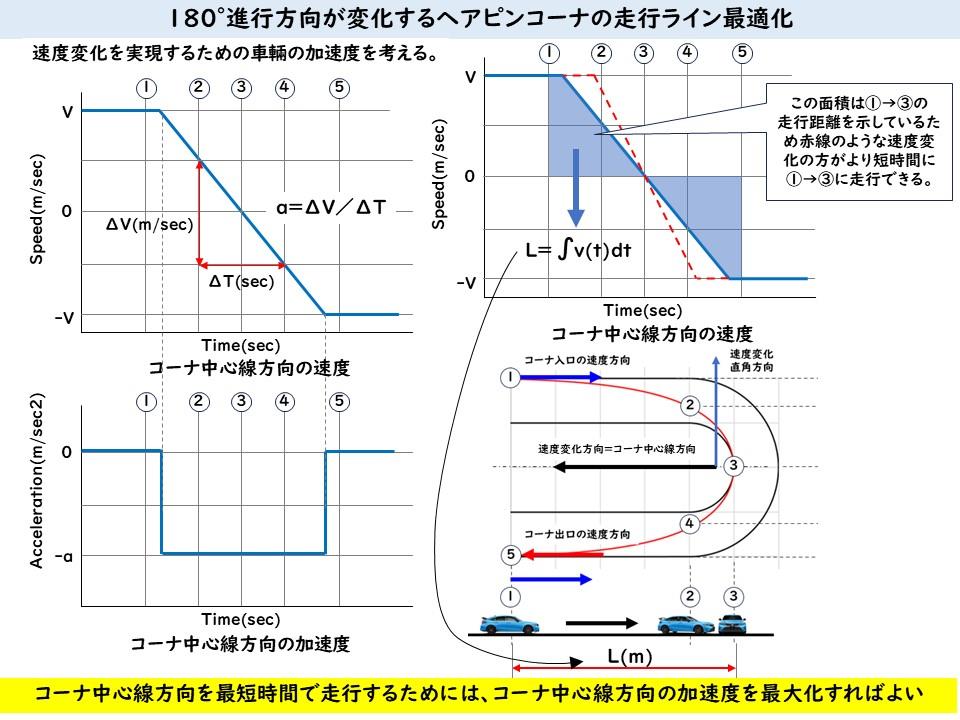
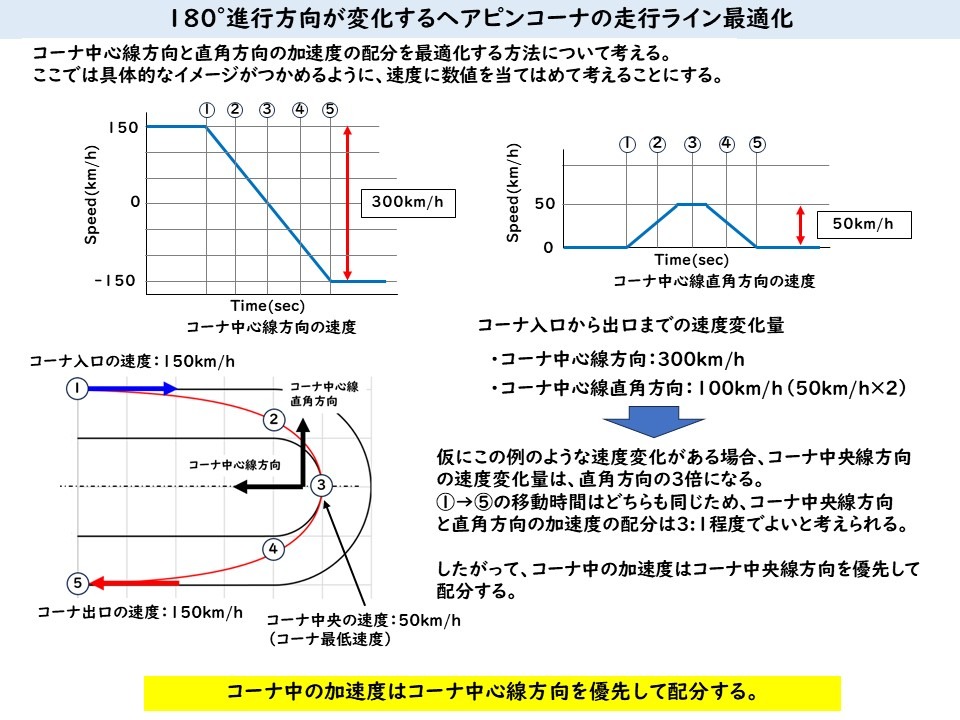
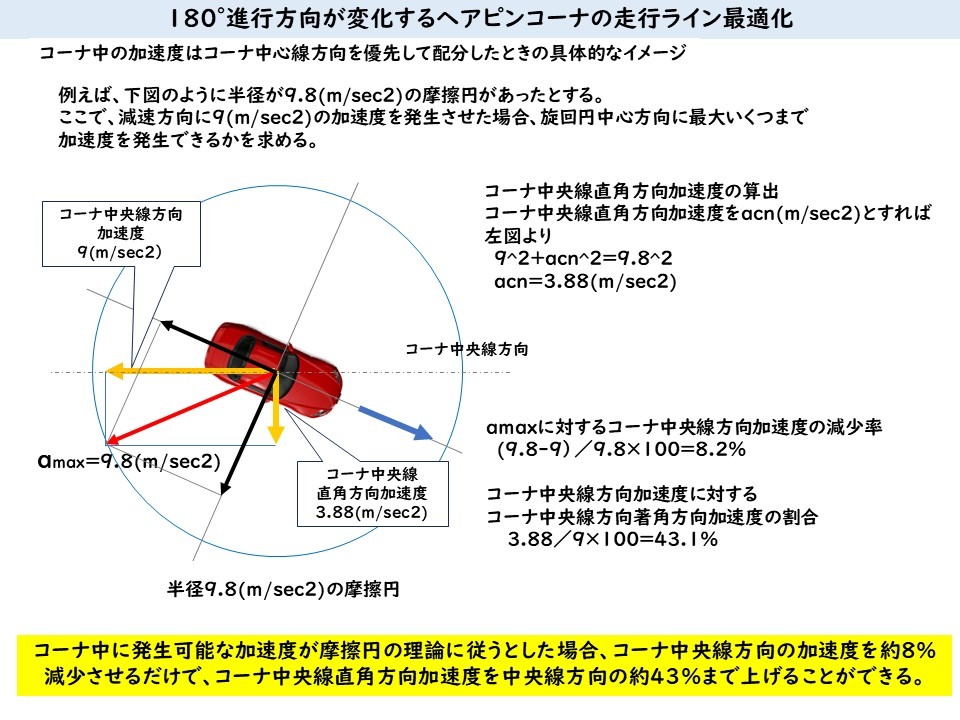
前回までは走行ラインの最適化するための速度変化、車輛加速度の大きさと方向、コーナ中央線方向とその直角方向の加速度(タイヤの摩擦力)配分について説明してきました。
僕は、随時サーキットシミュレーションの結果を見ながら考えているので、イメージがわくのですが、概念だけ説明されてもイメージがわかないと思います。
そこで、今日はサーキットシミュレーションの結果を使って説明したいと思います。
説明に使うサーキットシミュレーションのコースは以前作った単純形状の180°ヘアピンコーナです。→
こちら
シミュレーションの条件については以前に対し以下の変更をしました。
１）最大減速G：1.0G (前回0.95G)
２）最大横G：1.0G (前回1.05G)
３）最高速度：200km/h
減速Gと横Gは摩擦円の半径を1.0Gの真円にするためです。
加速側は変更していません。
最高速度は減速開始位置での速度違いが発生しないように200km/hで頭打ちになるように制限しました。
今回は、以前のシミュレーション結果から、①今のところ最も減速区間が速いR25 140、②最も加速側が速いR25 90、そして今回の理論説明用の走行ラインとして③コース内最大半径のR40の3種類を比較します。
①R25 140 (現時点の減速側最速ライン)
②R25 90 (現時点の加速側最速ライン)
③R40 (コース内の最大半径)
それと、今回の説明については本来は減速側と加速側の両方について考えるべきですが、加速側にまで手が回らないので、今回は減速側についてのみの説明です。
まずは走行ラインです。
次に横軸が距離、縦軸が車輛進行方向の速度のグラフです。
見やすいようにR25 140とR25 90を比較します。
（実際はコーナ中央までの距離が異なるため、どちらもコーナ中央を850mとして、中央で距離を合わせて比較しやすくしました。)
後から出てくる中心線方向の比較では横軸を時間にした方が理解しやすいため、横軸を時間にした車輛進行方向の速度グラフも作りました。
（このグラフも比較しやすいように、どちらもコーナ中央を18秒として中央であわせました。)
コーナ中央までの減速側時間差は0.08秒で、R25 140の方が速いという結果です。
速度変化のグラフを見てもR25 140の方が速そうなことはわかりますが、なぜこのような速度変化になるのかがいまいちわかりません。
そこで、コーナ中心線方向の速度と加速を見てみます。
今回のシミュレーションでは摩擦円半径を9.8m/sec2(1.0G)としているので、コーナ中心線方向の加速度も最大で-9.8m/sec2を超えることができません。
したがって、コーナ中心線方向の加速度が-9.8m/sec2に近ければ近いほど最大の加速度で減速できているということを示していて、速度変化は-9.8m/sec2一定減速時の速度変化に近づきます。
(文章中の加速度の大小は加速側も減速側も絶対値の大小です。)
R25 90は14～16秒区間の減速Gが小さく、その結果速度変化も-9.8m/sec2の線から離れています。
前回の説明に書いたように、このグラフの減速開始から速度0km/hまでの時間と速度でできる面積が減速区間の距離となっているため、同じ時間ではR25 90の方がR25 140に比べて走行距離が短い(減速区間が遅い)ということがよくわかります。
引き続きコーナ中心線直角方向のグラフを見てみます。
コーナ中心線直角方向の加速度を見ると、14～16秒のR25 90の加速度が高いことがわかります。
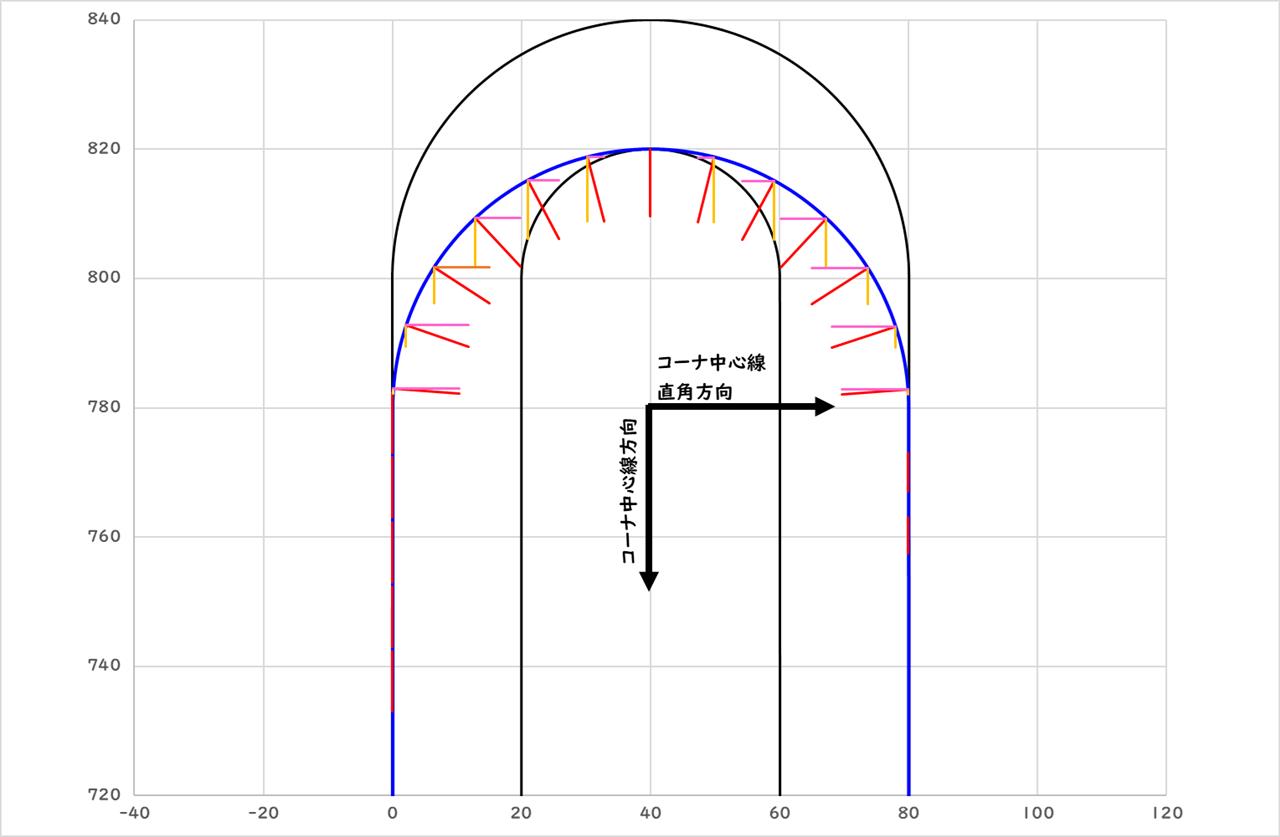
15秒地点の加速度を図で表すと、下図のようになります。
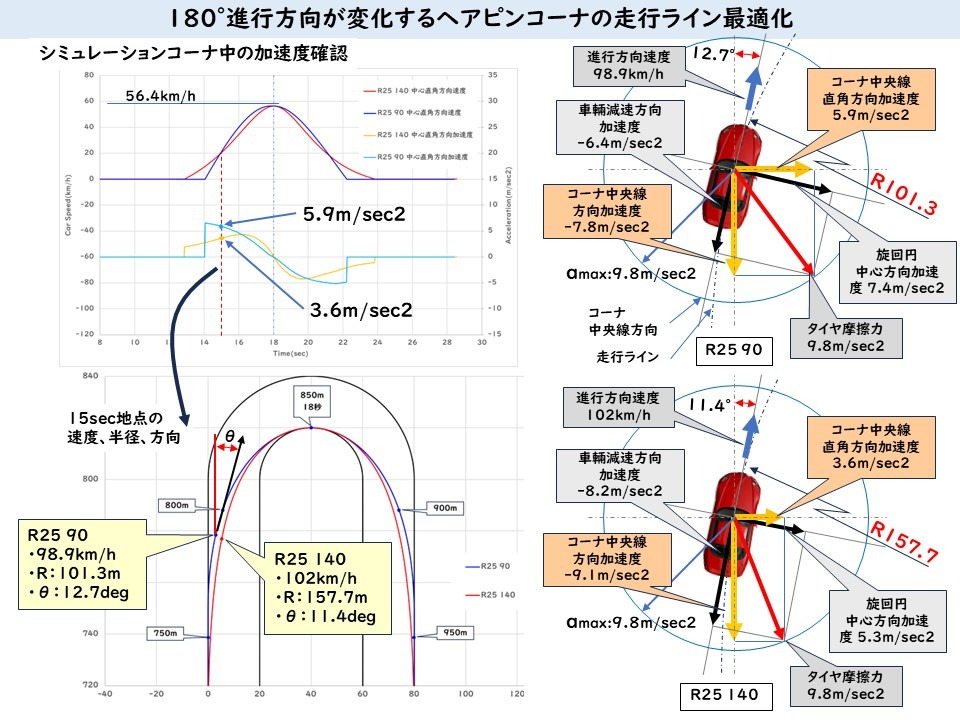
この区間の速度と半径を比較すると
R25 140 速度：102km/h、
半径：157.7ｍ、横G：5.3m/sec2
R25 90 速度：98.9km/h、
半径：101.3ｍ、横G：7.4m/sec2
となり、横Gの大きさの差はほぼ半径の差であることがわかり、横Gの大きさの差が中心線直角方向の加速度の大きさの差になっていて、それがR25 90の中心線方向の加速度を低下させる原因になっていることがわかります。
この結果より、車輛の進行方向と中心線方向の角度が小さいときの旋回半径を小さくすると中心線方向の加速度を低下させる原因になるということがわかります。
次はコース内最大半径のR40とR25 140のシミュレーション結果を見てみます。
R40はコーナ中は車輛進行方向に対し加減速をせず、タイヤの摩擦力は常に横方向に100%使っており、コーナ中の速度も他の二つと比べて高いです。
コーナ中の速度が高いにも関わらず、コーナ中央までの区間タイムはR25 140と比べて0.62秒も遅くなっています。。
今までは、このコーナ中の速度が高いがタイムが遅い理由を「距離が長いから」と考えていました。
それも間違ってはいませんが、いまいちスッキリ説明ができません。
そこで、今回の”コーナ中心線方向の速度変化グラフ”で比較をします。
見た瞬間にR40が遅いことがわかります。
R40は曲がり始めの15～17秒付近までのコーナ中心線方向の減速Gが小さくなっており、減速開始から16秒付近までの速度が低くなっています。
その結果、同じ時間ではR40の走行距離が短い＝コーナ区間が遅いという状態になっています。
先ほどと同様にコーナ中心線直角方向の速度と加速度変化および、15秒地点の各方向の加速度を図で確認します。
また、R25 140の減速開始地点である12.1秒からコーナ中央の18秒までの走行距離についても確認します。
コーナ中心線直角方向の速度、加速度変化を見るとR40が遅い理由がよくわかります。
まず、R40は旋回半径が大きいので、車輛進行方向コーナ最低速が他の二つのラインと比べて高くなっています。
コーナ中央のコーナ中央線直角方向の速度は、コーナ中の車輛進行方向最低速度と等しいため、コーナ中央線直角方向では曲がり始め速度0km/hからコーナ中央速度まで加速しなくてはなりません。
車輛進行方向のコーナ最低速度が高いということは、その分コーナ中央直角方向へ大きな加速度で加速する必要があります。
コーナ中央線直角方向へ大きな加速度で加速するということは、その分コーナ中央線方向の減速加速度が小さくなるということを意味しています。
コーナ中央線方向加速度が小さいのでその分コーナ中央まで走行する時間が多くかかりコーナ区間が遅いということになります。
R40(半径最大)はタイヤの摩擦力を横方向に100%使っているのにどうして遅いのだ！と疑問に思う方もいるかと思いますが、その理由は「コーナ中央線直角方向に無駄に加速して無駄に減速する代わりにコーナ中央線方向に加減速していないから」ということです。
サーキット走行も、仕事も、勉強も、間違えた方向に全力でがんばっても得られるものは少ないということになろうかと思います。
こうやって、コーナ中心線方向(入口と出口の速度変化方向)の速度変化および加速度を見ることでどちらの方が速く走れるのかがわかりやすくなりました。
ということで、180°ヘアピンコーナの場合、コーナ中心線方向の速度変化を最短時間で行う走行ラインが最速、最適化された走行ラインであるとなんとなくわかったということにして、そうすると実際の走行データではどうなっているのだろうか？と思うと思います。
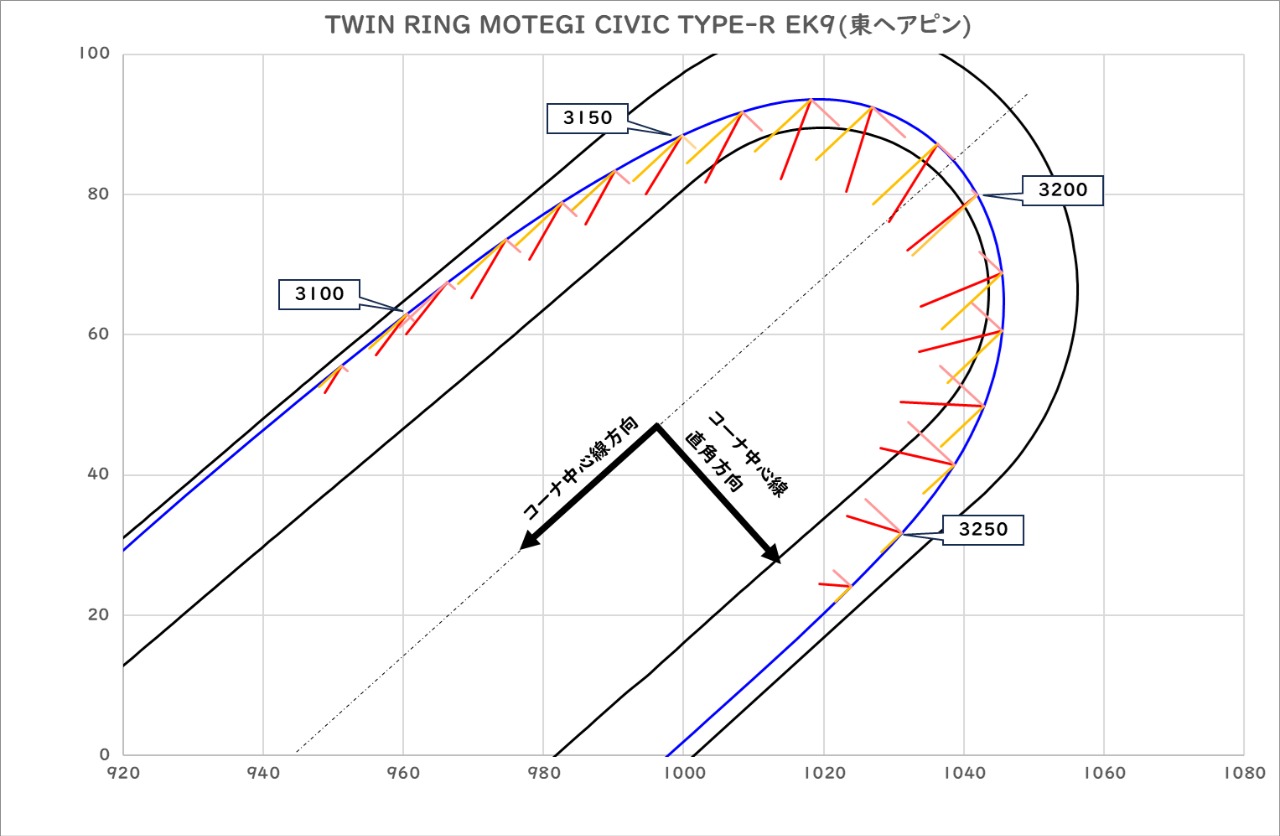
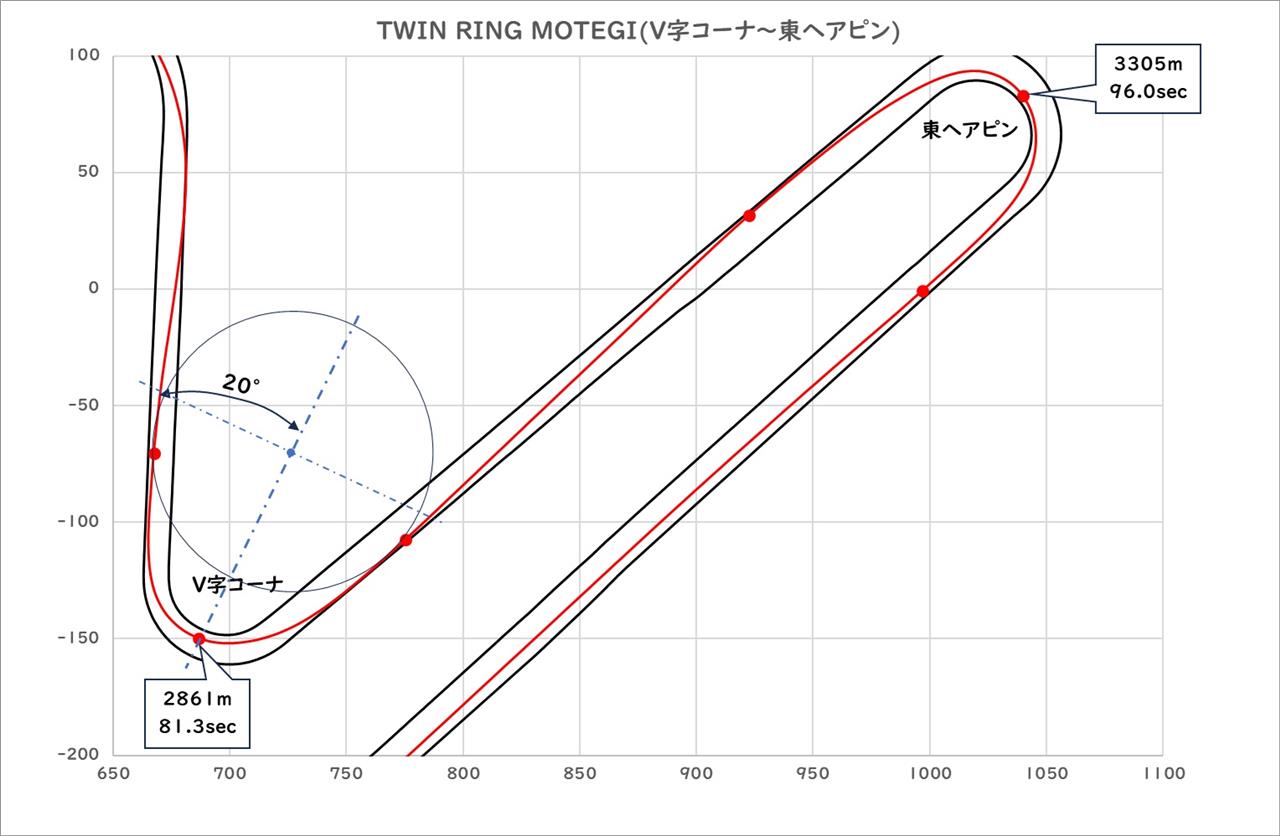
ちょうどいい走行データとして、昔登場した
N君BがEK9でツインリンクもてぎを走行したデータがあったので、次回はその紹介の予定です。
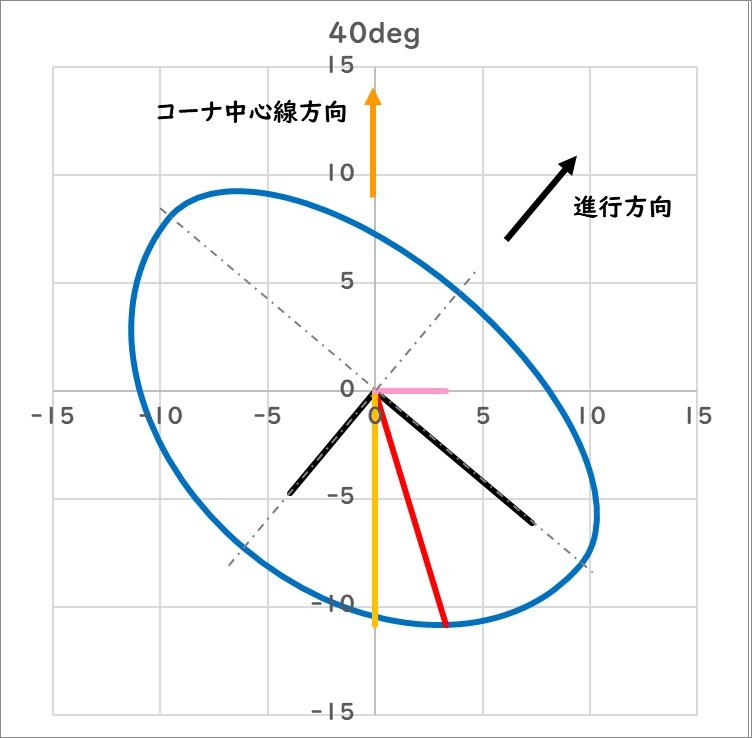
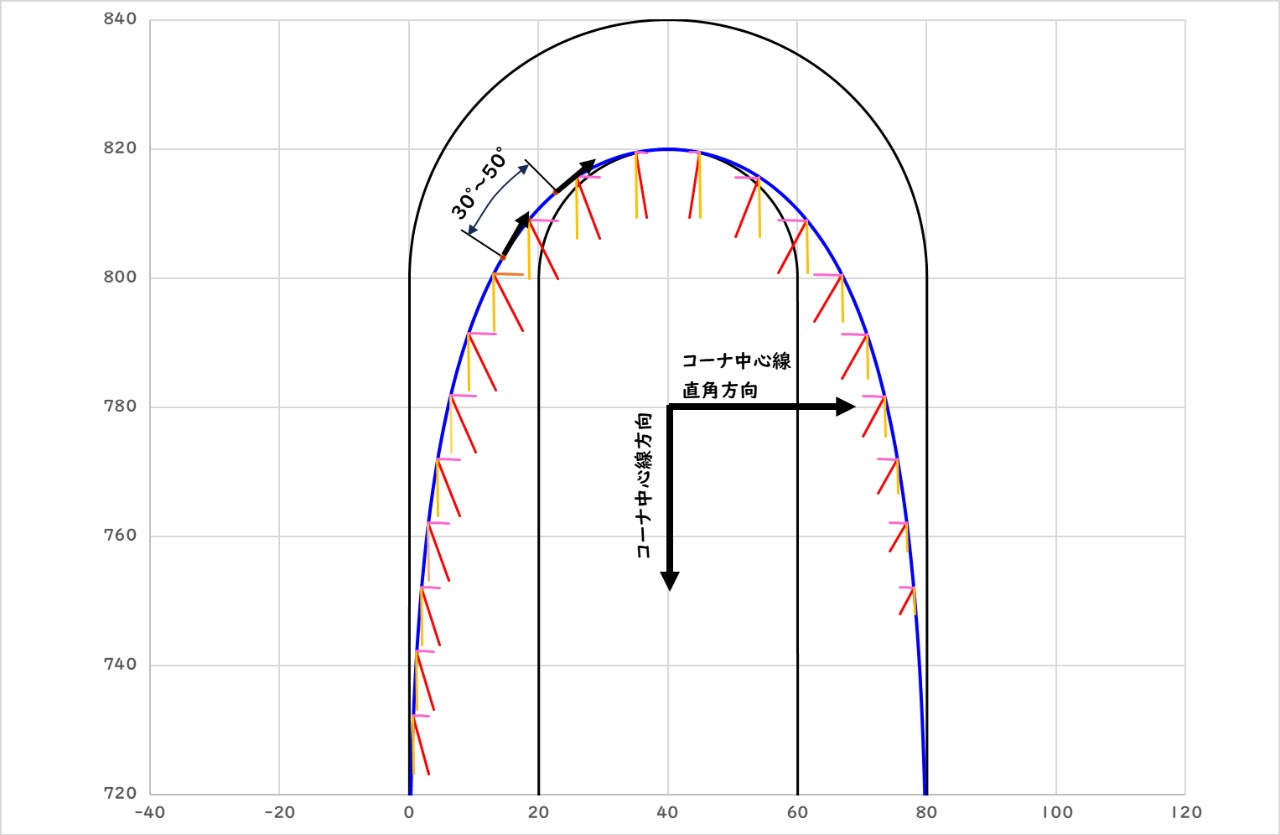
今回はコーナ中心線方向加速度の最大値の変化ついて考える予定でしたが、その前に各位置で中心線方向と直角方向の加速度の大きさと方向がどのように変化するのか絵的に確認することにしました。
