 謎の削除と登録www
謎の削除と登録www 



 ちょwww(PC)
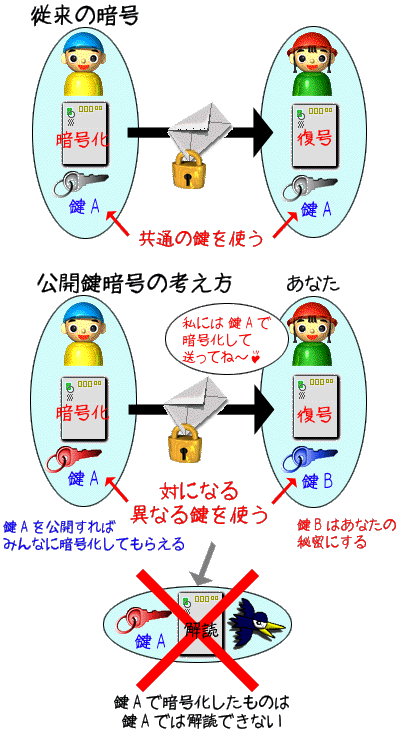
ちょwww(PC)  容疑者Aの本能 ≡ 数学者Bの挑戦 (mod盗難車Xのメッセージ) (PC)
容疑者Aの本能 ≡ 数学者Bの挑戦 (mod盗難車Xのメッセージ) (PC) 












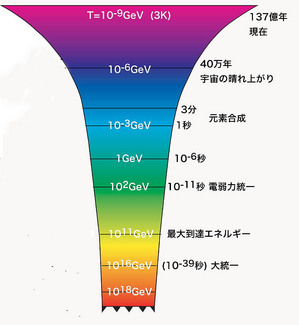
 未来へ行ける!?
未来へ行ける!?  2011年新年明けましておめでとうございます。
2011年新年明けましておめでとうございます。



 聖なる赤!?
聖なる赤!?  皆さん、メリークリスマス^^
皆さん、メリークリスマス^^|
Google Android Auto カテゴリ:その他(カテゴリ未設定) 2023/04/22 14:28:56 |
 |
|
備忘録、 TT第4回目オイル交換 カテゴリ:その他(カテゴリ未設定) 2023/04/21 18:06:56 |
 |
|
不明 大陸製 ルーフレール カテゴリ:その他(カテゴリ未設定) 2023/04/18 08:27:17 |
 |
 |
アウディ Q2 21年モデルにMCしたらTTから乗り換えで購入したいと思います。 A1からの乗換で当初は ... |
 |
アウディ R8 (クーペ) やはり普段乗る分にも快適に速いAudi技術の結晶 年式 : 2021年式 グレード : ... |
 |
アウディ A1 スポーツバック 街乗り専用車🚘✨✨✨ 2023年7月にQ2君と入替です🚘🚘 |
 |
アウディ R8 (クーペ) 街乗からサーキットまで優雅に熟すAudi技術の結晶 2日間お借りして、スーパーカーとし ... |
| 2024年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2023年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2022年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2020年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2019年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2018年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2011年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2010年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2009年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2008年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |
| 2007年 | |||||
| 01月 | 02月 | 03月 | 04月 | 05月 | 06月 |
| 07月 | 08月 | 09月 | 10月 | 11月 | 12月 |