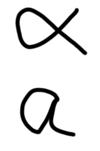Yuh_Fazioliのブログ一覧

　一つ前に取り上げた少数の筆算の例は、ツイッターで最近賑わわしているものである。

　何が話題になっているのかというと、値が整数になったとき、ゼロを消していない分マイナス1点されていたのが許せないと言うことらしい。


　小学校での筆算では、計算結果が整数になる場合は小数点以下を消すよう指導しているらしい。

　もっとも、筆算自体は計算手段であって、ここでの結果は単なる計算結果に過ぎない。この時点では小数点以下末尾のゼロがついていようがいまいが本質的にはどちらでも言い。

　最終的に整数である場合は整数として表記することにしているらしいのだが、それを筆算の結果でやる事を指導しているらしいのだ。

　それを問題にしている人たちによく見られるのは、数学的に正しいのに減点するとは何事かというものだ。

　数学的視点で見れば正しいのは間違いない。

　ただ、一般社会と数学の標準的取り扱いでは整数は小数点以下をつけてあらわさないことにしているから、それに合わせているにすぎないはずだ。

　整数だから整数と分かる形にしなければならない、という理由付けをする人もいるのかも知れないが、その辺の事情はいくらかあるのかも知れない。

　現実問題として、一般的な表記でない場合誤解されることがある。有効数字を表しているというのが最もありうる誤解だろう。

　それを避けるためにも、ゼロを消す一般的な表記を推奨した方がいいだろう。

　＊＊

　その指導方法がちょっと難しい。

　数学的には正しいのだから、減点されるいわれはない、と言う人は当然いるだろう。

　だからと言って誤解される表記を放置するのは、本人にとってもあまりいいことはないかも知れない。

　直して○、という手はある。

　ただ、現実の子供たちは○がついていると直されたことを気にかけないことが多い。

　そこで少々の減点をする、ということは行われやすいだろう。

　しかしそこで「数学的に正答なのに減点されたら傷つく」と言う人もいる。

　ここで評価とは何なのかという問題が出てくる。

　＊＊

　評価と呼んでいるものには二通りの意味がある。


　一つは指導する側が、指導がどの程度定着したかを調べるために行うもの。当然指導内容に即したテスト等で評価を行う。指導していないことはテストも評価もできない。

　もう一つは生徒自身がどの程度新しいことを身につけたか、あるいはどの程度の能力を持っているかをあらわすためのもの。これは指導内容を超えていればそのことも評価に加えることができる。

　日本の学校教育ではどちらかというと前者の意味合いが強い。

　日本の教育が与えたものをどの程度忠実に再生できるかを重視しがちであることとも関係するかも知れない。

　ともかくも、前者の視点である限り、指導方法に即した答えでないものは評価が低くなる。しかしこれは本人の能力を評価しているわけではない点に注意が必要だ。

　指導結果を知るためのものを本人の成績として渡すことに不自然さがある。

　実際には小学校などでは観点別評価であって、点数は評価に直結しない。

　＊＊

　一方で、本人の学力や能力を知りたいというニーズもある訳だ。これは指導結果の評価だけでは測れない。

　国際学力調査は、それに当たると考えても良さそうだ。

　＊＊

　「減点されるのが許せない」というのは、テストの成績が本人の能力を評価しているという前提でしかあり得ない感情である。

　指導効果の評価の場合、指導と異なる解答の仕方をした場合、指導が身についていないとしか評価できない可能性があるが、それは必ずしも本人の発想や能力とは関係がないのだ。だからゼロつけたからと言って正解であることが本人に伝わってさえいれば、この指導効果の評価が減点されたからと言って全く気にする必要が無い。しかも学問的に正しくても減点されたことに合理的理由あってのことだと伝われば、その減点の理由も内面化されやすいだろう。


　日本の学校では不幸なことに、指導効果測定の点数を非常に重視し、それを本人の能力、成績としてとらえてしまいがちだ。
　実際の成績は小学校等では観点別評価であるからその点数は直接表れることは無い。数学的に正しいが指導と違う回答をした場合もそれが評価テストには現れるかもしれないが成績にマイナスに反映する必要はないのだ。

　成績に反映されないのであれば、評価テストが減点されても、何も気にする必要はない。日本の評価テストの意味を知れば、その得点にこだわることがばかげていることに気付くはずだ。


　評価というものがどういうものなのかが分かっていればいいのだが、日本は得点主義が強く、ペーパーテストの結果を極めて重視する。

　本来そのようなものではない評価テストが本人の能力テストととらえられてしまっているための不幸であると言える。

　そんなばかげた得点主義自体を止めればいいのだ。


　指導効果測定のスコアが低くても、それとは異なる評価軸で成績がつけば問題ないのだ。

　観点別評価は評価テストの点をそのまま成績としない評価である。


　指導自体で教師が想定した考え方以外の考え方も評価することが昔から議論されていて、掛け算の順序問題はその典型だ。

　そうした先人の努力にもかかわらず、うかつな教師やそれが利用する教材会社の評価テストによって、指導した順序を守ったかどうかを評価点にしてしまうことを行うことがあるらしい。それは不幸なことだが、そもそもその日本の学校教育で行われる評価は指導効果を図るための一面的なものに過ぎないことが了解されるべきなのである。

　指導効果測定テストの点数で能力を測っているという理解が改められるべきなのだ。

　＊＊

　しかしながら、観点別評価を嫌がったのは何よりも子供の親である。得点主義に毒されていることと、客観的な能力把握ができないという問題の両方があるのだろう。日本の得点で入学の可否を決める入試制度がその背景にあるのは間違いない。

　子供の自由な発想を評価するには、指導効果評価の重視を止めなければならないし、入学試験で得点で切り捨てる日本的なしくみを止めなければならない。

　海外では入学は容易だが卒業は難しい制度になっている。日本はその逆で、得点を取ることにすべてのエネルギーが傾けられやすい。さらに大学で充分学んでいなかったとしても大学入学時の得点能力が就職でも評価対象に採用されるのだから、日本社会の考え方が病んでいる以外の何物でも無い。だから得点にこだわらざるを得ないわけだ。

　一方、小学校は特に生活上のニーズで教育が行われやすいので、必ずしも能力の学問的評価と一致するとは限らない。それも了解する必要があるし、能力評価を別に行う必要もある。

　そもそも指導効果測定を捨ててしまえば、きわめて柔軟に子供の能力を評価することができる。

　＊＊

　教師も指導効果測定をどうかすると本人の能力測定と思い込んでしまっていることがある。
　能力評価を行うには、教師が本質的な学問を理解しているかどうかが極めて重要である。また、何のためにこのような指導をしているのか、理解していなければ話にならない。

　まとめれば、

・日本の学校教育で行うテストはあくまで指導効果測定。本人の能力測定ではない。
・本人の能力評価ではないことが周知される必要がある。
・親も子も得点主義を捨てるべき。
・本人の発想を活かしたり、与えられたものを再生するのではない能力を育てる教育に移行し、指導効果に縛られない本人の能力評価を充実させる必要がある。
・そのためには入試制度を根本から見直し必要がある。

　こんな所だと思われる。



　

　以前の学校でも最近になって突然増えたし今の学校でも見かけるのが、小文字のａをアルファと書く生徒。



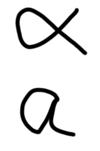
　下が筆記体のａだが（字が汚いのはご容赦）、上のアルファを「これが私のａだ」と言うのである。

　試しにアルファを書かせると、同じ文字を書く。全く区別がつかない。

　英語の教員に聞いてみると、中１でちゃんと教えているのに何故かアルファと書く子が出てくるのだという。

　活字体の［ａ］を真似た字を書いてアルファと区別がつかない字体になっている可能性があるのだが、活字体のａともまるで違う。αにしか見えない

　女子に多く、かつての丸文字の様に、ファンションとしてとり入れられているのかも知れない。

　文字だけに、他の文字と区別がつかないものは許容しがたい。

　＊＊

　生徒と同じように、αのようにかいてもアルファと区別する必要が無いなら構わないと主張する人がネットにいたのだが、年齢不詳ながら他人を片っ端から喧嘩をふっかけ、罵倒し、幼稚な論理を振り回し続けているので相手するのもばかばかしくほっておいた。ネトウヨによく似た行動様式だ。

　文字の基本は何より他の文字と区別がつくことだ。区別しがたい文字はあえて区別できる様に注意を払う。

　量の単位リットルの記号は本来国際的な取り決めであるＩＵＰＡＣでは小文字のエルでありｌと規定されているが、それでは数字の１と区別がつきがたいので大文字のＬが許容されている。単位で大文字が使われるのは人名由来の場合なのだが、大文字になってしまったので学者がジョークでリットル氏の物語を作ってしまったという話があるぐらい特別な措置だ。
　単位に筆記体を使う事は許容されていないので、かつてよく使われていた筆記体の「ℓ」は許容されていない。今売られている製品や出版物ではほとんどが大文字のＬでリットルを表示している。

　それぐらい区別は重要だ。

　大人が書いて、区別がつかなくてコミュニケーションに不都合をきたしても本人の自己責任だが、さすがに教育段階ではそうも行かない。他人に消去法で解読させなくてはならない様なことを放置するわけにも行かないので区別がつく文字を書く様に言っておいた。

　ネットにはこう言うことを必要もないことを押しつける「強制」と言って非難する人間がそこそこいるらしい。

　自分の考え方こそが正しい、現実世界とのすりあわせは必要が無いと思っているらしい。

　＊＊

　たとえば、小学生の算数では、４という数を扱うときは４と表記するよう指導しているらしい。４．０が筆算で出てきてしまったら４に直して扱う。

　分数でも分母と分子が同じになったら整数に直す。４／４という表記も当然あるが、まずは割り算ととらえて割り切れれば整数として取り扱う。このときわざわざ４．０とかと書く意味はどこにも無い。割りきれる数は整数であるから、整数を小数点をつけて無意味なゼロをつける理由はないのである。

　これは一般的な数学での数値の表記でもあるし、世間一般での表記の原則でもある。

　理系で数学以外の人間にとって、

　　２．５
＋ １．５
-------
　　４．０
ではなく

　　２．５
＋ １．５
-------
　　４

とやられるとぎょっとするが、そもそもこの演算で与えられている数値に有効数字としての意味があるかどうか不明なので４．０が正しいと主張することは間違っている。

　しかし、数学では原則として４で表記する。もちろん前後にゼロをつけても同じ意味だが、ふつうあえてやることはしない。　ゼロをつける理由が数学には存在しないからだ。

　数学的には０００００４も４も４．００００も等価だが、普通は見やすく、無駄のない４と書き表す。

　しかし、実験系では測定精度を桁数で表す有効数字という概念であつかう。このため、

１．０００
を
１とか１．０とかと表記すると測定精度が本来より低いものとして受け取られる。ゼロに意味を持たせているのである。


　もちろん電卓は勝手にゼロを省略するし、エクセルも明示的に桁数を表示するように指示しない限りゼロを省略するのがデフォルトになっている。

　一般の人間にとって最もなじみのあるあらわし方だ。


　小学校での表記は、原則小数点以下の末尾のゼロは表記しない。１は小数ではなく整数だからだ。数学の標準的な表記に合わせているし、社会一般での表記でもあるからともいえる。

　ここであえて４．００などと表記することは、有効数字としての意味があるかのようにも見えてしまう。

　例え数学的に正しくとも、現実の生活の中で不都合をきたす様な表記は避ける指導が望ましい。４．０と書いても×ではないが、誤解を受けることを伝えておくべきだろう。

　数学的な正しさを言うなら、２進数を１と０であらわしたときの１００（いちぜろぜろ）も４と等価だが、もちろんこんな表記を断りもなく使えば１００と誤解される。

　数学的正しさが、かならずしも生活の中でも問題ないとは限らないので、すこし制約する指導をしておいた方がいい。

　特に小数点以下のゼロは有効数字の扱いと重なるので有効数字を扱うまでは避けた方が望ましいだろう。

　＊＊

　小学生にも数学的に正しいものは無条件にすべて認めるべきだという数学概念絶対主義者がそこそこ見られるが、小学校は社会生活を学ぶ場でもある。

　数学的な正しさを認めた上で、生活の上で誤解が無い表記を身につけさせる意味が無いとは全く思わない。

　数学好きの人間の中に、現実とのすりあわせは不要、自分の論理さえ正しければ問題が無いという人間が時々おり、その人間が身勝手な行動を取り、他人を傷つけたり嘘を平気でついたり、迷惑をかけたりすることをたびたび見てきた。
　そう言う人間だからこそ純粋数学という論理のみの世界に浸りたがり、現実の方を批判すると言うことがおこりやすいのかも知れない。

　思いこみやバイアスで批判していることすら見られる。
　

　そういう人には社会生活を学ぶ場でもある小学校教育は理解できないことだろう。小学校教育は生活、身近なことからスタートする。いきなり６０進法を学ぶのも時計を読めるようにするためだ。

　掛け算順序問題が変な話になりやすいのは、純粋数学に浸りたがる人々のメンタリティも関係しているのかも知れない。

　ホント私嫌なんだよね、掛け算順序問題。

　伝統的な掛け算順序問題と違う話を、現実を無視して勝手に脳内事実を作り上げてそれを根拠にものを言う人たちがいて、排他的で攻撃的で、いかにもネットなので。

　困ったことに、そう言う議論に何らかの研究者が巻き込まれて、事実でないことを事実と思い込んでものを言っていることが。

　とある理系ではない研究者が最近この問題をやたらにツイートしているのだけど、彼も例によってネットの一派の思いこみを事実ととらえて、算数教育がおかしい云々と言っている。聡明な人がこの問題を理解できないのはおかしいとか。いや、聡明でないのはあなたなのだけど。

　＊＊

　掛け算の導入段階で、仮に順序を決めてそれに当てはめて立式するトレーニングをやる事を、小学校で掛け算の順序を定義して押しつけているみたいに言うのがよくある例。

　この方法は、戦後の算数の歴史の初期段階からあって、おそらく日本人の大部分がやって来たやり方で、しかも日本だけではなく海外でもよくやられている。

　掛け算という概念をはじめて学ぶ上で、「○○個のものを××倍」という身近でよく扱う課題を例に立式するわけだけど、どうかすると、掛け算は2つの数を×の両側におきさえすればいいと、闇雲に出てきた数字を並べてしまうことが起きる。立式に必要な数値ではないものがあっても、何も考えずに入れてしまったりする。それでは掛け算の概念が理解できているとは言いがたい。
　実際に行う操作を、発想することが比較的自然な順番で立式することを通じて、掛け算とはどんな操作をするものなのかを身につけることが目的であるはずだ。

　だから、もし逆に立式したとしても、本人がその順番でどういう操作をしているのかを説明できれば問題が無い。きちんと理解した上で指導している教員は、そうしているはずだ。算数教育としては決して順番を押しつけているわけではなく、操作と言語と立式を一致させて、式を立てるという難しい課題を扱いやすくしようとしている。

　これをやらないと、単に掛け算が操作手順を暗記する機械的なものになりかねない。
　そろばんができても、暗算ができても、それは操作手順に基づいた扱いをおぼえるだけで、数学的理解とは関係ないのと同じことになる。

　＊＊

　２点問題があって、一つは実際の現場では一斉授業なので、子供たちがどういう発想の元に立式したのかを発表する機会が少なく、画一的に与えられた順番を守らせる指導が起こりうること。小学校の教員はすべての教科を教えるために、理系出身者が少ない現実もあり、どうかすると理系科目への理解が低いまま取り扱われていることがありがち。

　もう一つは、誤解の元に、過剰に定義の様に扱ってしまう教員がいるらしいこと。与えられたルールを何も考えずに守ろうとするのは、極めて日本的かも知れない。頭の悪い人間ほど、単純なルールを何も考えずに内面化し、他人にも適用させようとすることがあるが、そう言うケースなのかも知れない。

　この問題を取り上げる人のすべてが、掛け算の数学としての取り扱いをマスターしていて何の疑問を持ってない故に、導入時の困難を理解できず、さらにその導入時に交換法則込みで教えることを根拠なく可能だと思い込んでいること。

　単純に操作だけなら掛け算を身につけるのは難しくない。しかし、現実の操作を自分で立式することは掛け算を習い始めたばかりの、掛け算の概念も身についていない子供には難易度が高い。

　ひとつひとつ段階を踏んで、理解の幅を広げていこうということなのだけれど、それが掛け算を既にマスターしてしまい、そう言う段階を踏んで身につけたことをすっかり忘れてしまっている人たちには理解できないらしいのだ。

　自分は掛け算を理解しているから、子供たちも最初から同じレベルで扱える様にするべきだ、っていう一種の暴論なのだよね。

　足し算に順序をやたらに強調するのは私も賛成はしないけれど、掛け算についてはまずは操作と立式の順序を一致させて、掛け算という概念がどういう操作を扱うものなのかを整理する機会を作った方が身につけやすいと思っている。

　面積で扱うと、自動的に交換法則も成り立つことが分かるのだけど、掛け算をならう段階では面積を扱えないから、面積を扱う段階で順序にこだわることは無意味であることが分かればいいことになるけれど。

　＊＊

　数学的概念だけで物事を扱えると思い込んでいる人は時々いるのだけれど、その人が現実に使っているのは、人間に取り扱いやすい「文字」を使い、指の本数に起因する「１０進法」であったりする。

　人間にとって扱いやすい様に数学概念に制限を加えているのだけれど、ほとんどの人はそのことを意識せずにものを言っている。

　掛け算初学者にとって、どう扱うことが導入しやすいのかを考えることは必要で、時に数学概念に制限を加えた状態で扱った方が理解しやすいことがあるだろう。

　普通、自然現象を扱うグラフでは横軸に時間を取る。数学的には軸に何を取ろうが構わないのだが、目が横に移動しやすい人間にとって、我々にコントロールできない時間を横軸に扱った方が取り扱いやすいらしい。
　これに文句をつける人はそうはいない。こういう取り扱いが一般的なのだ。

　数式の中で「１×」は自明なので省略する。もちろん数学的には「１×」が入っていても全く問題ないのだが、自明なものは見た目に邪魔なので省略してしまう。これも普通は文句をつけない。

　数学的には０００００００９６と表記しても９６と表記しても９６．０００００００００００００と表記しても意味は同じだが、分かりやすい様にゼロは消してしまう。これも普通は文句をつけない。

　一次方程式、二次方程式、三次方程式と順を追って扱うことに文句をつける人もいないだろう。それぞれ包含関係になっていて、三次方程式を扱えば自動的に他も扱えるとしても。


　人間は、数学概念を扱うとき、自分たちが分かりやすいやり方を採用し、それになじんでいる。時にそれは数学概念に制限を加えた扱いをしているけれど、それはわかりやすさと引き替えにされている。特に学ぶ段階ではより簡単な形で扱う。

　べつに小学生に数値を教えるとき、数学的には８進法や２進法で教えてもいい訳だけど、１０進法と６０進法しか扱わない。共に人間がなじんできたものだからだ。当然数学的発想を制限することになるけれど、それを云々する人はよほど変わった人だ。

　しかし、なぜか掛け算の導入段階で制限を加えた形で掛け算を扱うことに慣れることを、発想を制限するといきり立つ人たちがいる。

　自分の理解のレベルでしかものを考えられないとしか言いようがない。掛け算は誰もがマスターしている概念なので、文句をつけやすいのだ。

　＊＊

　最近、筆算で

　　 １．７
＋　２．３
-----------
　　 ４．０

と答えたら減点された、というtweetを見ていきり立っている人たちがいる。

　筆算は途中計算式みたいなもので、小数点以下のゼロは書いても書かなくてもいい。ただし、数学的には数値の前のゼロや小数点以下の末尾のゼロは省略することが一般的なので、ゼロを消す指導をしている。

　ところが実験系の人たちがこれを見ていきり立った。有効数字を無視していると。
　自分も直感的にはそう思ったが、よく考えてみればこの計算で小数点以下の桁数が違う場合、有効数字の概念を知らないのに、ゼロをどこまでつければいいのかを小学生が判断することはできないと思い直し、そもそも筆算で出てくる小数点以下のゼロは、操作上出てくるだけのもので、有効数字とも、数学の扱いとも異なるものに過ぎないと気付いた。

　筆算で出てくるゼロは、有効数字とは異なるものだ。だから、有効数字を理解していないこの段階では、数学での取り扱いであるゼロ省略で扱った方が、意味なくゼロを付加して数値を扱いにくく表記したり、一件意味ありげに見えて無意味にゼロをつけられた数字を表記することを避ける上でベターではないかと思われるのだ。

　しかし、有効数字を半端に知っている人たちの中に、我慢ならない人たちがいるらしい。それはそもそも有効数字として扱っていないものを許容することだと言うことに気付いていないらしい。

　有効数字とは、どの桁までが実測数値として意味があるかをあらわした取り扱いだ。単純に小数点以下何桁とつかうものではない。最小目盛りの１／１０が有効数字の桁数を決めるとか、そう言うものだ。

　先の筆算の、１．７という数値がそもそも有効数字込みの表記なのかどうかも分からない（実際は１．７０かもしれないし、２かもしれない）のに、勝手に４．０が有効数字であると思い込んでいるに過ぎない。数学には有効数字という概念での取り扱いは普通しないのだから、勝手に有効数字だと思い込んで４．０を許容するのは有効数字での数値の取り扱い自体に誤解を与えかねない。

　数学的には、００４でも４でも４．０でも４．００００００００００００でも数値としては等価だ。桁数に一切の意味は無い。




追記：
　この問題に首を突っ込んでくる、割と直情的にものを言ってしまう人たちのメンタルの方が興味がある。
　ある有名な人物は、算数教育では虐待が行われていると言っているのだが、事実誤認がいくつも見られる。
　自分は覚えてないだけで、現在数学としてのルールや実験系の有効数字の扱いを内面化していても、その前の段階があったはずなのだ。それなのに、自分が内面化しているものだけを正義として、自分がたどってきたはずの段階を踏んでいる部分を記憶にないばかりに「そんなコトをやることがおかしい」と全否定している。

　じゃあ、はじめて掛け算に出会うこどもたちにどうやって数学的な扱い方を意味理解を含めて指導していくのか、考えてみればいい。日本語すら怪しいこどもたちに、いきなり交換法則を教えてもそれは意味理解にはつながらない。そもそも掛け算というのは何なのかを教えなければならないのだ。身近な事柄をベースに具体的操作を通して立式に結びつけていく過程はどうしても必要だと思うかどうか、是非考えてほしいものだ。

　対案を出せ、というのはこういうときに言うべきこと。もしよりベターな対案が出てくれば新しい教え方というものが定着する可能性は出てくる。




　

　

　20年以上昔、生徒に暗号文を渡され、解読してみてと言われたことがある。

　そこそこ長い文章がいくつも含まれている様だ。

　それを丹念に見ていくと、どうも日本語の文章をそのまま何かのルールで置き換えた様な特徴がある。

　もしこれが何らかのルールで単純に置き換えただけなら、頻出しやすい助詞に目をつけていけば、置き換えルールは見つけやすいだろうと。

　「は」とか「を」とかはよく出てくるわけだから、手がかりにしやすい。

　そうやって行くと、おぼろげながらルールが見えてきた。

　細かいことはよくおぼえていないが、五十音表を数文字分シフトするタイプの暗号だった様な。

　そう時間をかけず解読して翌日生徒に見せたら驚いていた。

　「簡単だったか！」といわれてしまったが、如何に単純でも、推測を手がかりに解読するのは、初めての人間にはそう簡単ではない。


　ただ、ルールを見抜けるのはそのための情報である暗号文が長かったからであって、これが極短いものだったら解読は困難だっただろう。

　ヒントは与えすぎない方がいいというのは、一つの教訓かも知れない。

三字熟語ゲーム
http://www.gamedesign.jp/flash/sanjuku/sanjuku.html


　これ結構はまる。

　三字熟語を作るのは結構頭の体操になる。

　正解ではないけれど、意味の通った三字熟語もできてしまって、面白いというか悔しいというか。

　＊＊

　やっているうちに、NHKの連想ゲームという番組を思い出した。テーマ曲や台詞がよみがえってくるんだよね。

　ヒントをもとにした言葉当てゲームなのだけど、壇ふみさんと大和田獏さんの名勝負があったり、当時はさえていた水島裕とか、訳の分からないことを言うことが多かった江守徹とか、懐かしい。

　動画があった。



　徳田章さんの1990年のものだから、随分新しいものだけど。

　シンプルだけど面白い。